On a fabriqué une corde dont la longueur est exactement celle de la circonférence de la Terre à l’équateur. En supposant qu’on la rallonge d’un mètre et qu’on lui fasse faire le tour de l’équateur, toujours à égale distance de la surface de la Terre (on supposera qu’elle est lisse!), quel est le plus grand animal qui pourrait passer sous la corde? Une fourmi? Un lapin? Un tigre? Un éléphant?
Détails sur ce problème ici ⬇️.

Avant de poursuivre votre lecture, je vous invite à tenter de résoudre le problème par vous-même. Vous serez alors assurés que votre raisonnement et vos stratégies ne seront pas influencés par ce qui suit. Si vous ne l’essayer pas par vous-mêmes maintenant, vous pourriez avoir des regrets dans les jours à venir! Voilà, vous êtes avertis! 😁

Le rayon de la Terre est environ de 6378 km à l’équateur (source : Wikipédia). Nous pouvons donc calculer la circonférence de la Terre à l’équateur.
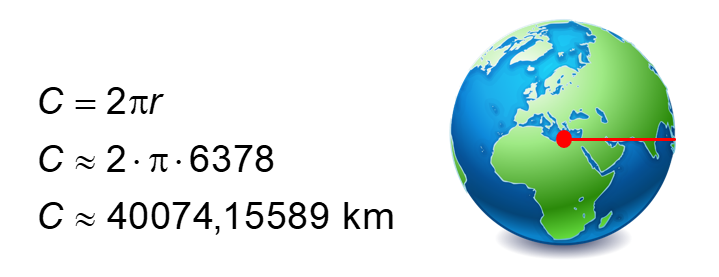
Nous ajoutons 1 mètre à cette mesure soit 0,001 km pour trouver la circonférence du cercle créé avec la corde allongée.
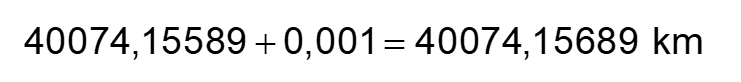
Faisons maintenant le chemin inverse. À partir de la nouvelle circonférence, déterminons le rayon de ce nouveau cercle.
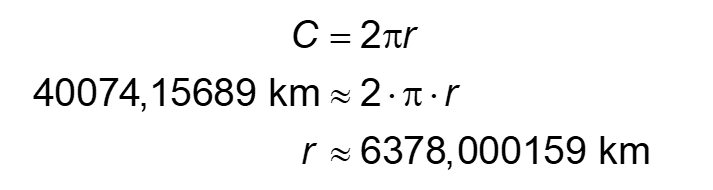
Nous connaissons maintenant la longueur du rayon correspondant au cercle formé par la corde allongée. Il ne reste plus qu’à déterminer la différence avec la mesure du rayon du cercle initial afin de déterminer l’espace entre les deux cercles.
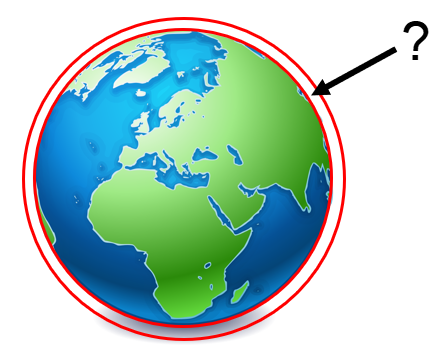
Roulement de tambours! 🥁🥁🥁
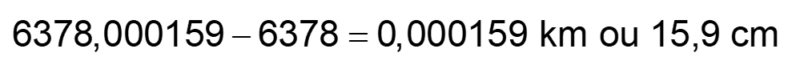
Il y aurait donc un espace de presque 16 cm, espace où un lapin pourrait facilement passer! 🐇
La réponse est contre-intuitive d’autant plus qu’elle ne dépend pas du rayon de la Terre. La réponse serait la même peut importe la taille de la sphère utilisée : une balle de tennis, une autre planète, un petit pois, etc.
Vous pourriez faire vivre le problème à vos élèves avec quelques objets sphériques ou cylindriques et une corde (ballons de basket-ball, rondelle de hockey, pièces de monnaie, cercles tracés sur le plancher du gymnase, etc.). Il sera évidemment plus simple de travailler avec des objets cylindriques.
Algébriquement, on peut tenter de comprendre le lien entre les deux rayons et le fait qu’on ajoute 1 mètre à la circonférence.

Puisque nous savons que la circonférence du cercle final est 1 mètre plus longue que la mesure de la circonférence du cercle initial, nous pouvons donc établir que :
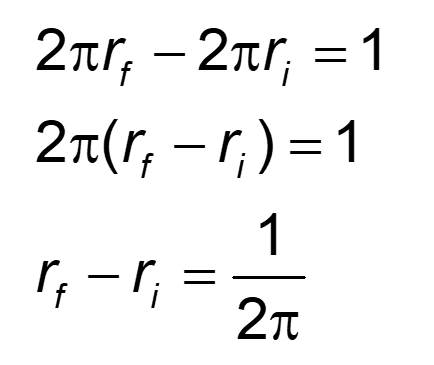
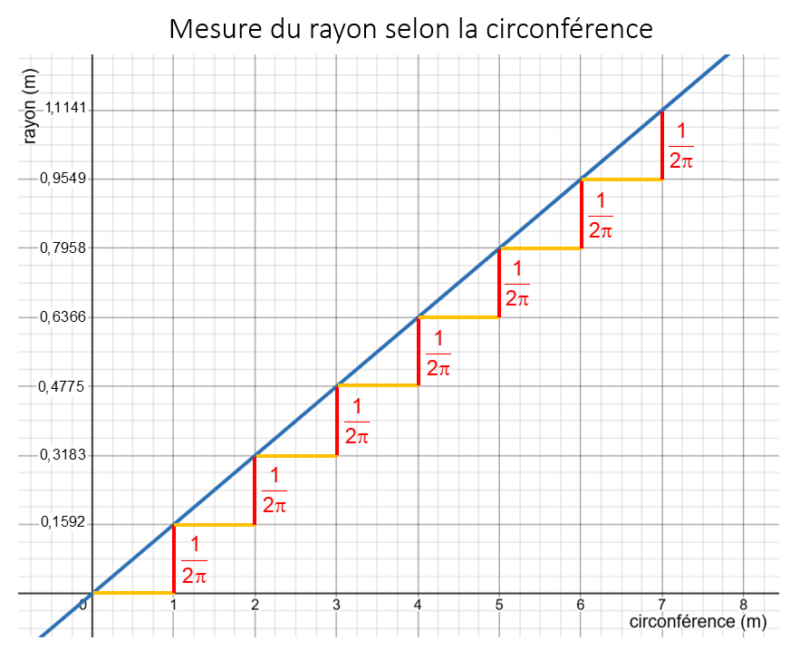
Une différence de 1 mètre entre les circonférences amène donc une différence de 1/2π entre la mesure des rayons, d’où le 15,9 cm. Chaque mètre de circonférence supplémentaire ajoutera 15,9 cm à la mesure du rayon et ce peu importe la mesure du rayon initial. Graphiquement, voici le lien entre la mesure de la circonférence et la mesure du rayon. On peut très bien voir qu’à chaque augmentation de 1 mètre de la circonférence, le mesure du rayon augmente de 1/2π mètre.
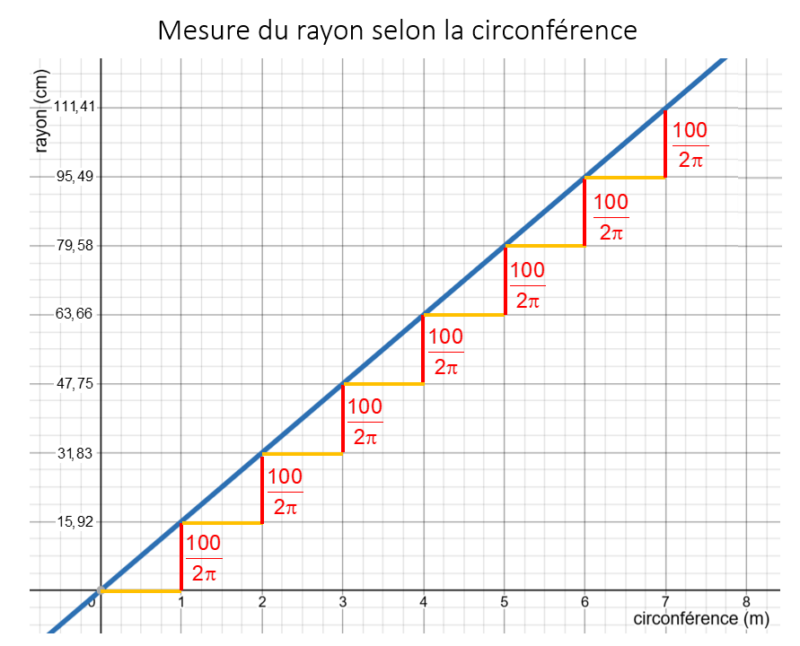
Voici le même graphique avec la mesure du rayon en cm :
Lien vers un Geogebra sur ce problème créé par Hugues Malherbe.
Prolongement : Quelle distance devrait-on ajouter à la corde initiale si on veut qu’un éléphant puisse passer sous cette corde?
Voici un autre problème utilisant des notions du cercle :
Si une horloge faisait la taille de la circonférence de la Terra à l’équateur, combien de kilomètres parcourraient les trois aiguilles en une seconde?
N’hésitez pas à m’écrire si vous avez des questions, des commentaires ou si vous souhaitez partager votre expérience après avoir utilisé ce problème avec vos élèves.
martin.roy005@csssamares.gouv.qc.ca
Lien vers un diaporama qui contient une bonne partie des images présentées dans cet article. (privilégier Microsoft Powerpoint).
Dernière mise à jour de cet article : 11 décembre 2024


