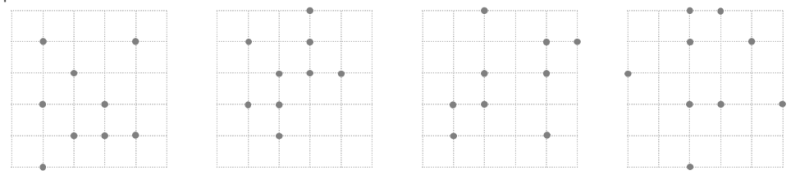
Pour travailler les définitions et caractéristiques des figures planes, les concepts d’angles, de droites parallèles et perpendiculaires et pour travailler avec des figures qui ne sont pas disposées uniquement de manière prototypique. Une activité qui est pertinente sur plusieurs niveaux au secondaire. Serez-vous en mesure de repérer les formes géométriques demandées?
L’objectif est simple : relier des points qui permettent de former la forme géométrique demandée. La tâche peut être très simple dans certains cas, mais vous verrez que ça se corse dans certains cas et vos connaissances des caractéristiques et des définitions des figures géométriques vous permettront d’être plus stratégiques.
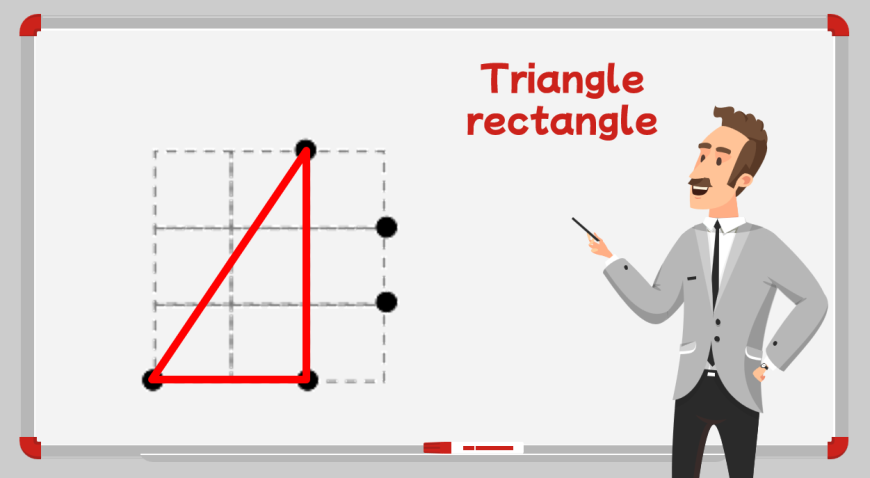
Par exemple, ce puzzle demandait de trouver un rectangle. À gauche, vous avez le puzzle et à droite la solution.
Vous devez maintenant trouver un parallélogramme dans les 4 puzzles suivants :
Assurez-vous d’avoir les bons arguments mathématiques pour démontrer que vous avez la solution. Ça ressemble à un parallélogramme ne sera pas suffisant comme argument… 😂
Vous trouvez cela trop facile? Essayez de trouver un losange dans le puzzle ci-dessous :
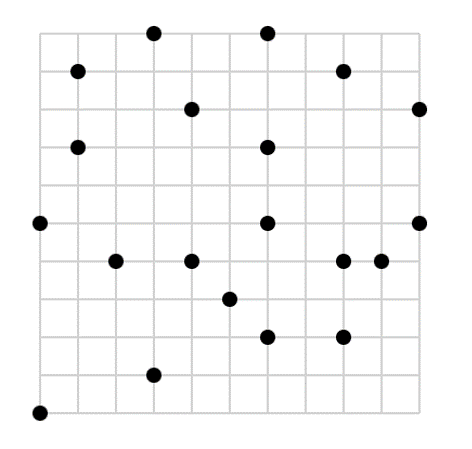
Vous ne l’avez pas encore trouvé? C’était pourtant si facile! 😁
J’ai créé le dernier puzzle avec un générateur de puzzles de Zukei. Vous pourriez vous-mêmes créer vos propres puzzle selon vos besoins ou les difficultés rencontrées par vos élèves. Voici le lien vers le générateur: https://www.primefactorisation.com/zukei/. Ce générateur a été conçu par Shaun Carter. L’objectif n’est vraiment pas d’amener vos élèves à ce niveau de difficulté; c’est simplement pour vous montrer qu’on peut rapidement compliquer l’exercice. Il est préférable d’y aller graduellement avec vos élèves et de mettre l’emphase sur ce qui est important : bien connaître les définitions et caractéristiques des formes géométriques.
Quelques ressources
Voici 42 puzzles à résoudre : Puzzles de Zukei.
Ces 42 puzzles ont été élaborés par Naoki Inaba. C’est lui aussi qui a créé les Puzzles de Mizu.
J’ai également réaliser un diaporama qui vous permet d’afficher la solution de chacun des ces 42 puzzles. Simplement à m’écrire si vous souhaitez que je vous le fasse parvenir.
Scott Miller a également créé une activité DESMOS à partir du document de Naoki Inaba.
3 autres documents PDF créés par Mark Chubb
Document #1
Document #2
Document #3
Un dernier document créé par Don Stewart.
Pourquoi réaliser cette activité avec vos élèves?
On travaille trop souvent avec des figures géométriques placées de façon prototypique.
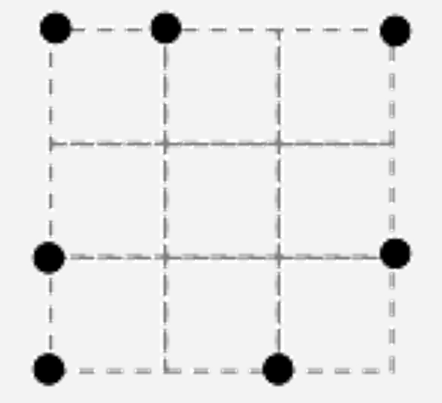
Qu’est-ce que ça veut dire prototypique? Voici des figures géométriques placées de façon prototypique :

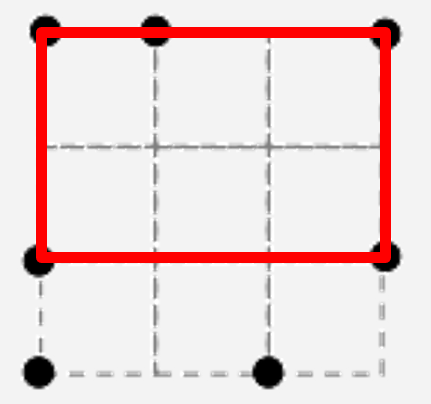
On peut apercevoir sur cette image un triangle rectangle, un rectangle, un parallélogramme, un carré, un triangle équilatéral, un hexagone régulier, un losange et un trapèze isocèle. Avez-vous eu besoin de réfléchir à leur définition ou à leurs caractéristiques? Il est probable que d’un simple coup d’oeil, vous saviez déjà de quelle figure il s’agissait. Pourquoi? Parce qu’on est tellement habitué de voir ces figures dessinées de la même façon (de façon prototypique) qu’on a pas vraiment besoin de réfléchir. Voici les mêmes figures placées différemment :

Donnez cette dernière image à vos élèves. Sauront-ils identifier le carré? Le losange sera-t-il identifié correctement ou on indiquera plutôt que c’est un parallélogramme. L’angle droit du triangle rectangle est-il évident? Pas vraiment. Il y a peu de chances qu’on identifie le triangle gris comme un triangle rectangle. Bref, en plaçant nos formes géométriques de différentes manières, on force ainsi les élèves à vérifier les définitions des différentes formes ainsi que leurs caractéristiques. Je vous invite à y penser lorsque vous tracerez des formes sur votre tableau.
Lorsque vous serez bloqués dans un puzzle de Zukei et que vous trouverez enfin la solution, il est fort probable que la position de la forme géométrique n’était pas prototypique. Vous aurez alors utilisé la définition de la figure et ses caractéristiques afin de trouver quels seraient les points à relier. Je vous avouerai que certains m’ont donné du fil à retordre!
En espérant que ces puzzles permettent à vos élèves de parfaire leurs connaissances en géométrie! N’hésitez pas à m’écrire si vous avez des questions, des suggestions ou des commentaires!