Un problème tout simple, mais avec un beau potentiel!
Les détails ici ⬇️
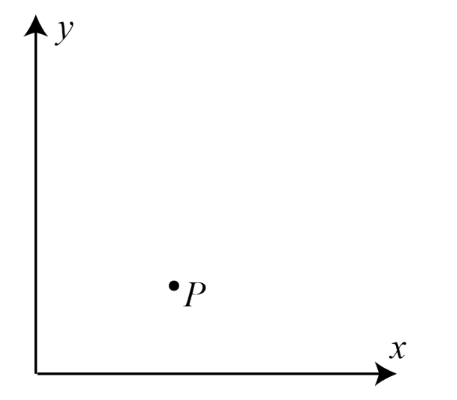
Voici d’abord l’énoncé du problème :

Lien vers le fichier à imprimer
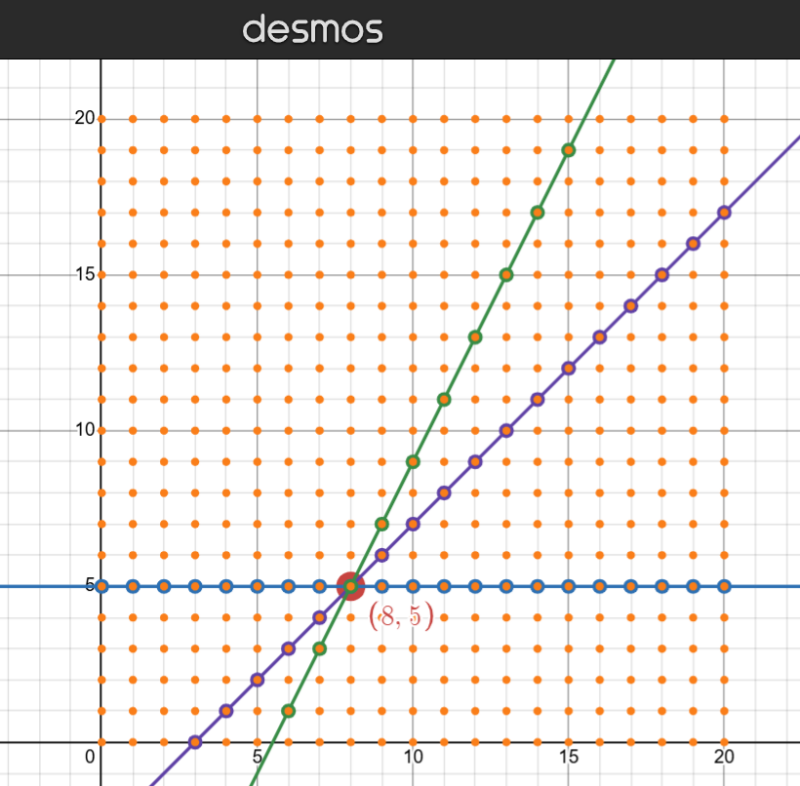
Voici un lien vers un DESMOS que vous pourriez utiliser pour effectuer un retour sur le problème ou que vous pourriez utiliser dans le pilotage.
Les points oranges représentent toutes les coordonnées possibles pour le point Q. Il y a au total 440 possibilités (21 x 21 – 1). Considérant que le point Q est un point différent du point P, c’est pourquoi on doit soustraire le point P des possibilités (d’où le -1).
Il y a 20 coordonnées possibles où la pente de la droite PQ sera de 0 (pente nulle).
Il y a 17 coordonnées possibles où la pente de la droite PQ sera de 1.
Il y a 9 coordonnées possibles où la pente de la droite PQ sera de 2.
Il y a donc 46 possibilités de coordonnées pour le point Q au total.
La probabilité que la pente de PQ soit de 0, 1 ou de 2 est donc de 46/440 (ou 23/220 ou 0,1045 ou 10,45%).
Si vous réalisez ce problème en classe avec vos élèves, je serais ravi que vous me partagiez vos commentaires, les stratégies mobilisées par les élèves, les difficultés rencontrées dans le pilotage et/ou par vos élèves, etc. Vous pouvez m’écrire à l’adresse suivante : martin.roy005@csssamares.gouv.qc.ca
N’hésitez pas à me partager vos questions ou des commentaires!
Une ressource très riche en problèmes!
Chaque semaine, le CENTRE d’ÉDUCATION en MATHÉMATIQUES et en INFORMATIQUE de l’Université de Waterloo partage de riches problèmes (pour la 3e à la 12e année). Les solutions de chacun de ces problèmes sont partagées une semaine plus tard.
Lien pour avoir accès aux problèmes en français
Lien pour avoir accès aux problèmes en anglais (vous aurez ainsi accès aux problèmes 11e/12e année)
Archives des problèmes des années 2022-2023 et 2023-2024 (français)
Archives des problèmes des années 2022-2023 et 2023-2024 (anglais avec les problèmes 11e/12e année)
Les archives contiennent également l’ensemble des solutions des problèmes!