Un groupe est formé de 12 personnes. Combien de poignées de mains différentes peuvent-ils s’échanger? Et pour un groupe de 20 personnes? Et pour des groupes de n’importe quelle dimension?
Pour plus d’infos sur ce problème ⬇️.
Ce problème qui peut paraître banal est très riche. C’est assurément un problème de type Low floor, high ceiling; c’est-à-dire un problème accessible pour tous les élèves et qui permettra à certains de pousser leur raisonnement très loin.
Différentes stratégies peuvent être mobilisées par les élèves. Parmi les diverses stratégies qui seront envisagées, certains seront tentés de commencer dès le départ avec des groupes de 12 personnes alors que d’autres pourraient essayer de répondre d’abord à la réponse avec des groupes de plus petite taille.
Certains voudront peut-être illustrer les poignées de main avec des traits qui relient des personnes (ou des points) comme dans ces images :
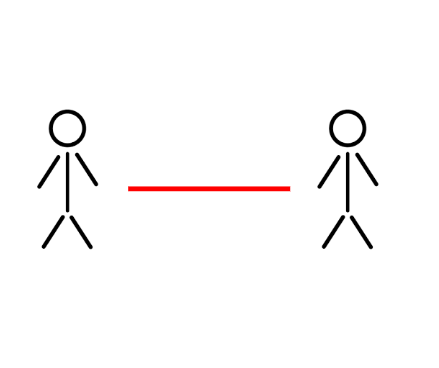
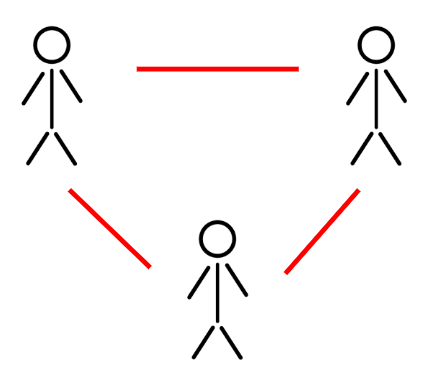
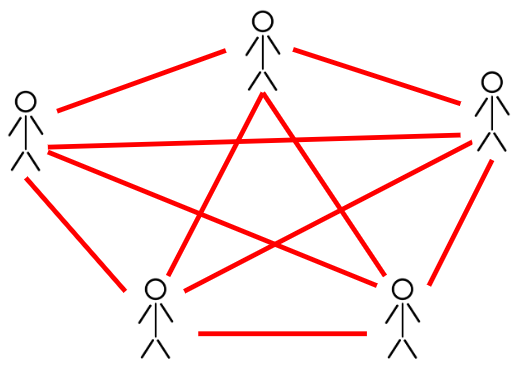
Dans les images ci-dessus, on peut déjà essayé de dégager une suite logique :
2 personnes : 1 poignée de main
3 personnes : 3 poignées de main
4 personnes : 6 poignées de main
5 personnes : 10 poignées de main
6 personnes : 15 poignées de main
et ainsi de suite.
Déjà avec ces nombres, on pourrait tenter de généraliser et établir une formule pour calculer pour un nombre x de personnes.
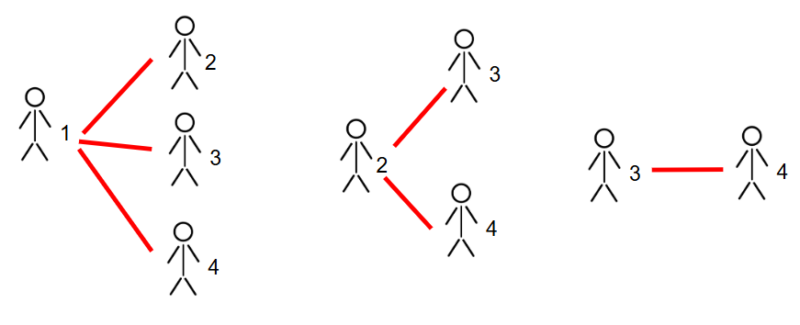
Une autre stratégie serait d’y aller une personne à la fois en se demandant à combien de personnes chacune devra-t-elle serrer la main. Dans l’exemple ci-dessous à 4 personnes, la personne #1 serre la main aux personnes #2, #3 et #4. La personne #2 ayant déjà serré la main de la personne #1 serrera la main seulement aux personnes #3 et #4 et la personne #3 serrera la main à la personne #4. On totalise donc 6 poignées de main différentes.
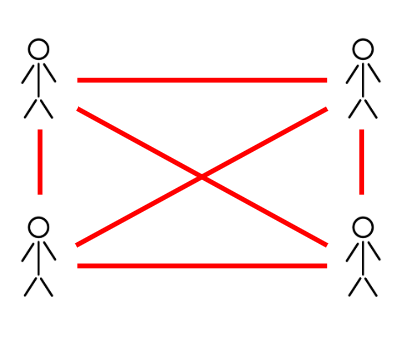
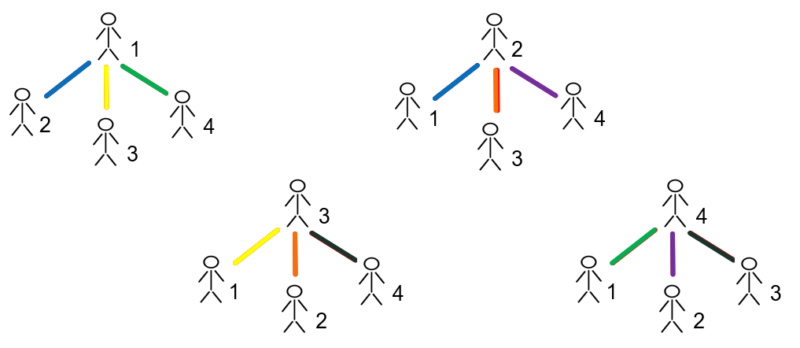
Une autre stratégie serait d’illustrer toutes les poignées de main qu’il est possible d’échanger entre les différentes personnes puis d’éliminer les doublons. Encore une fois dans l’image ci-dessous, vous avez un exemple avec 4 personnes. Il y a une possibilité de 12 poignées de mains, mais en éliminant les doublons, on se retrouve avec 6 poignées de mains « différentes » (représentées ici par des couleurs différentes).
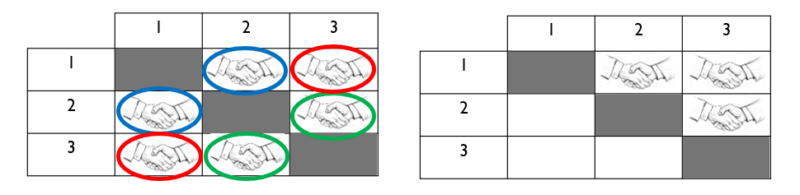
Finalement, une stratégie qui peut être très intéressante à exploiter est celle d’utiliser un tableau à double entrée pour illustrer les poignées de main. L’avantage de cette stratégie est qu’elle pourrait permettre plus facilement aux élèves d’observer le lien qui existe entre le nombre de personnes et le nombre de poignées de mains différentes et ainsi de généraliser pour des groupes de n’importe quelle dimension.
Par exemple, dans un groupe de 3 personnes, on peut observer dans le tableau de gauche que certaines poignées de mains se répètent. Les poignées de même couleur peuvent être considérées comme une seule poignée de main. Les cellules du centre son grisées puisqu’une personne ne se sert pas la main à elle-même! En éliminant les « doublons », on se retrouve donc avec le tableau de droite.
Vous pourrez voir dans les images ci-dessous le même genre de tableaux pour des groupes de 5 ou de 6 personnes.
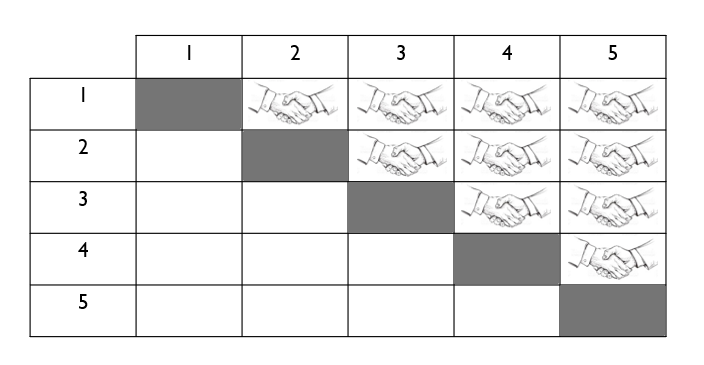
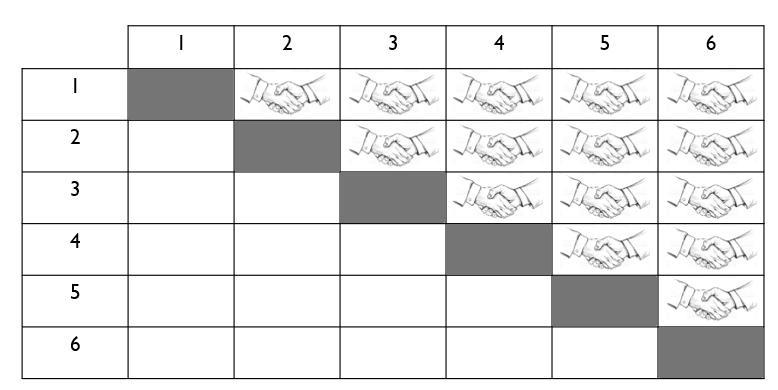
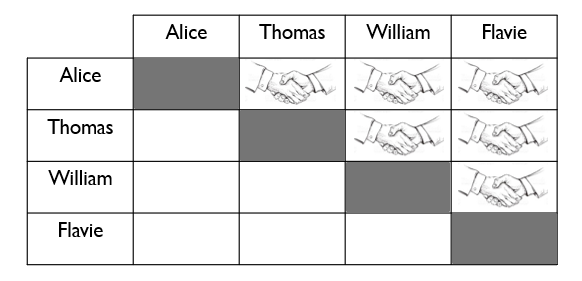
Remplacer les nombres par des des noms fictifs ou par les noms de ses élèves pourrait permettre de rendre le tout un peu plus concret.
En étant placées dans un tableau, on peut essayer de dégager la formule qui permet de calculer le nombre de poignées de main.
Prenons par exemple un groupe de 7 personnes :
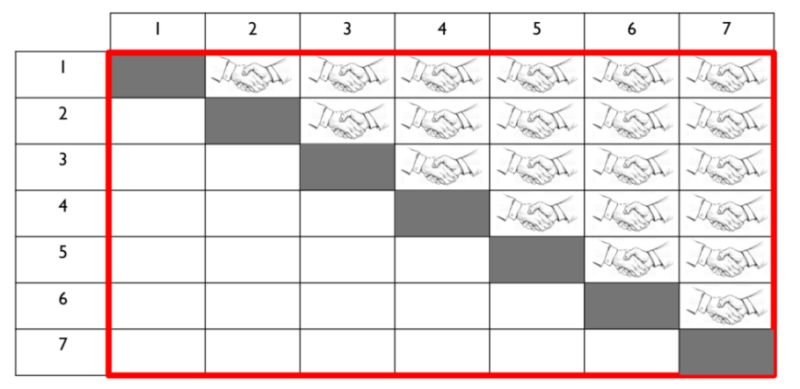
Si ce tableau était rempli de poignées de main, on aurait alors 7 x 7 poignées de mains. Par contre, on doit retirer les 7 poignées de main au centre du tableau (une personne ne se sert pas la main à elle-même) puis on doit diviser le résultat par deux pour ne conserver que les poignées de mains « différentes ». On a donc cette formule qui nous permet de déterminer le nombre de poignées de main différentes dans un groupe de 7 personnes :
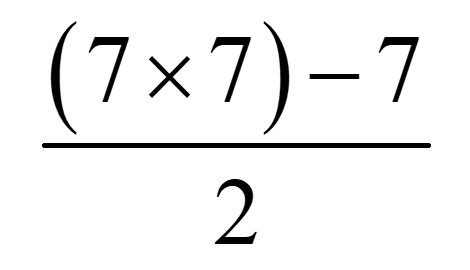
Et donc, en généralisant pour des groupes de n personnes, on obtient l’une ou l’autre de ces formules :
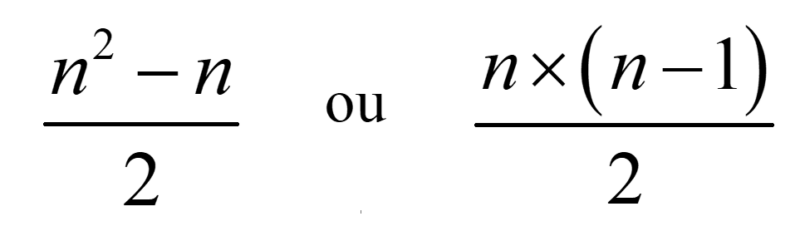
L’objectif n’est pas nécessairement d’amener tous les élèves à effectuer cette généralisation; cela dépendra évidemment du contexte et de votre intention pédagogique.
Lien vers le diaporama contenant l’ensemble de ces images et davantage (privilégier Microsoft Powerpoint pour que les animations fonctionnent correctement).
N’hésitez pas à m’écrire si vous avez des questions ou des commentaires!
martin.roy005@csssamares.gouv.qc.ca

