Un super problème pour les élèves de 4e secondaire SN! Plusieurs stratégies possibles! Au travail!


Avant de poursuivre la lecture de cet article, je vous invite à tenter de résoudre le problème par vous-même. Vous serez alors assurés que votre raisonnement et vos stratégies ne seront pas influencés par ce qui suit. Si vous ne l’essayer pas par vous-mêmes maintenant, vous pourriez avoir des regrets dans les jours à venir! Voilà, vous êtes avertis! 😁
Premier exemple de raisonnement :
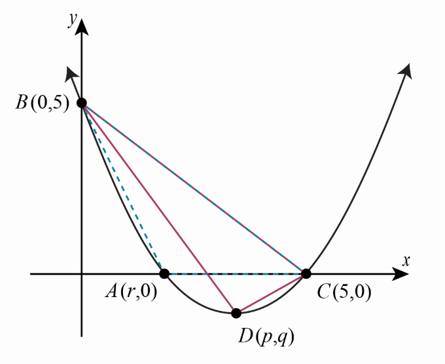
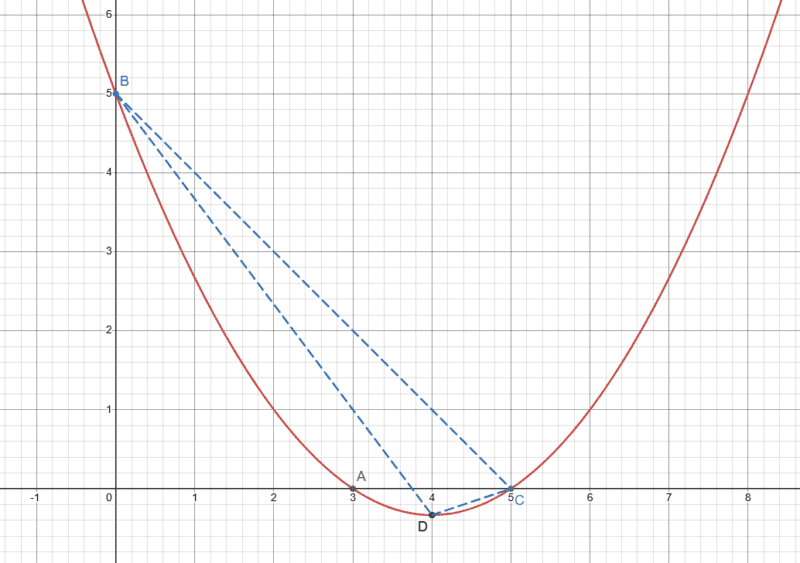
L’aire du triangle ABC est de 5 unités carrées.
En prenant le segment AC comme base du triangle ABC, on peut donc déduire :
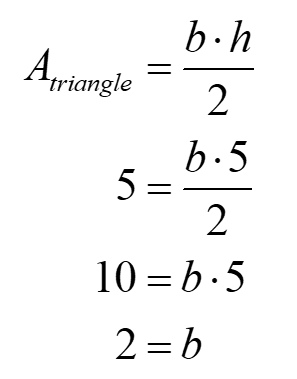
Les coordonnées du point A sont donc (3,0).
Les coordonnées du sommet sont donc (4,q).
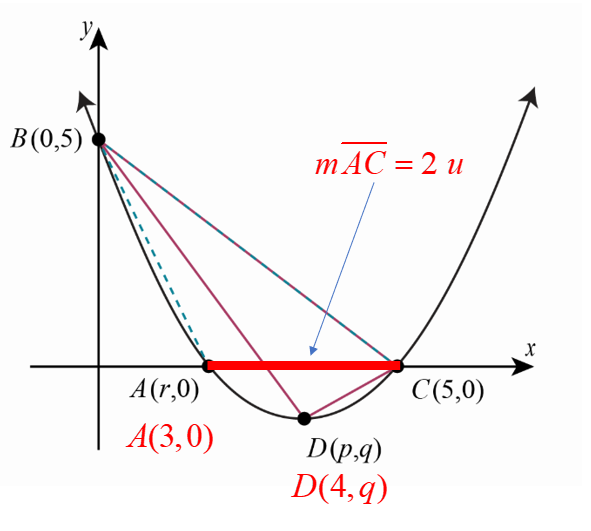
Trouvons l’équation de la parabole.
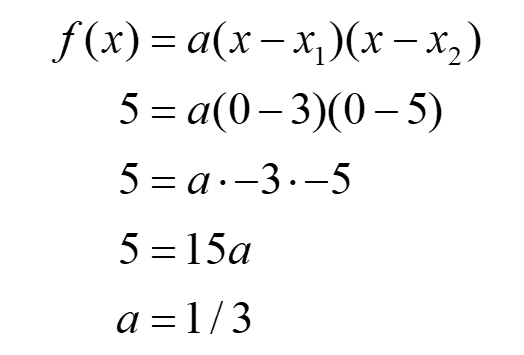
L’équation de la parabole est donc :
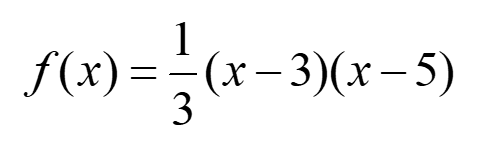
Trouvons l’ordonnée du sommet :
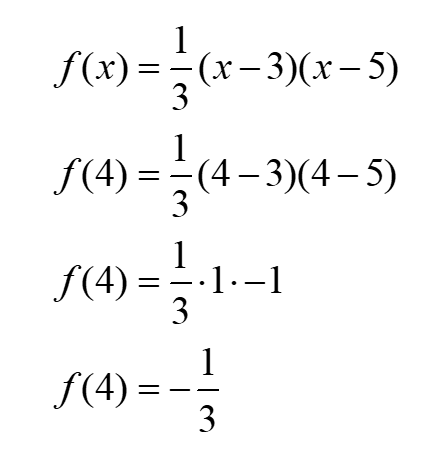
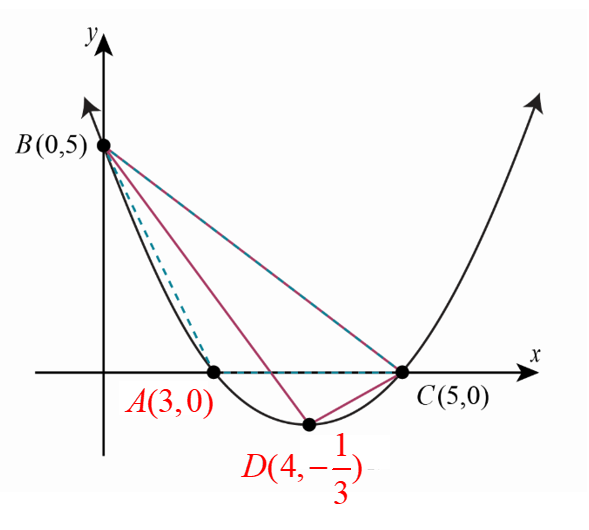
En ayant les coordonnées de tous les sommets du triangle DBC, on peut déterminer la mesure des segments du triangle.
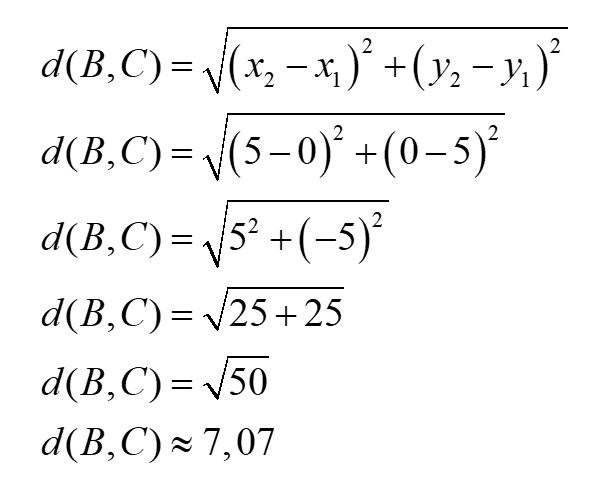
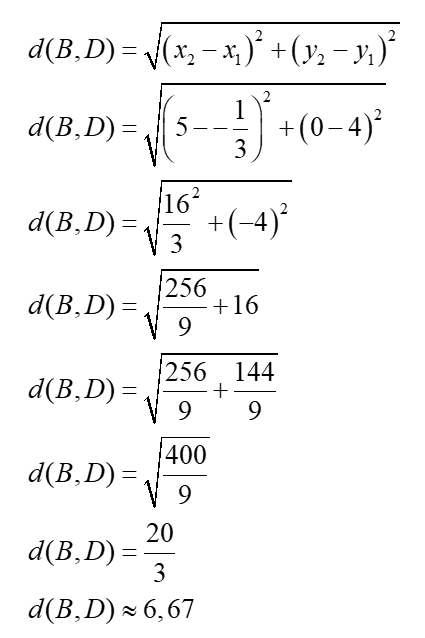
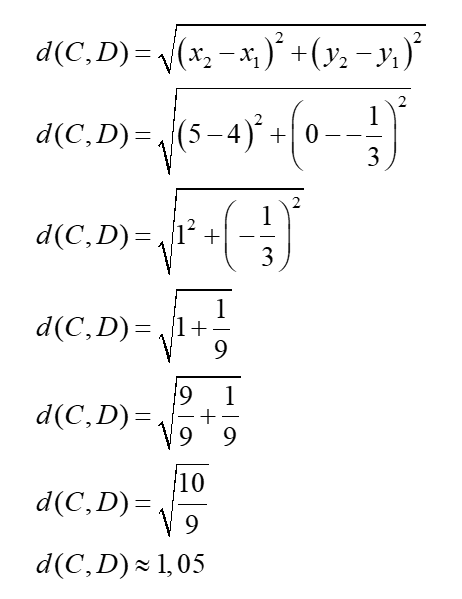
Finalement, nous pouvons déterminer l’aire du triangle DBC avec la formule de Héron.
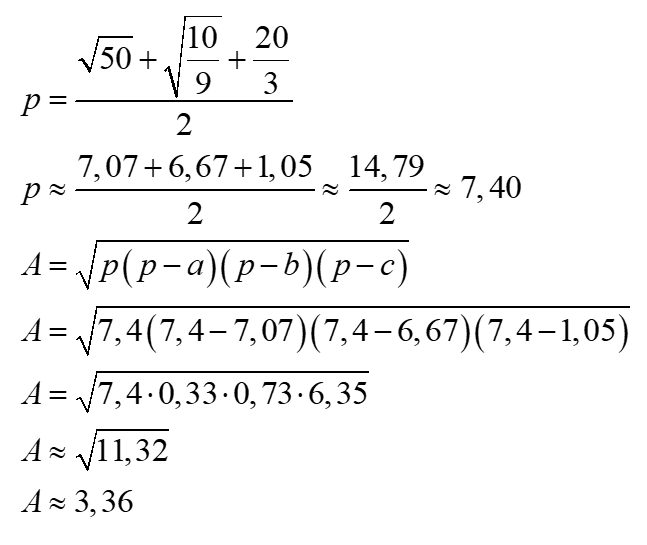
Autre raisonnement possible
Une fois que le sommet de la parabole est identifié, il est également possible d’utiliser ce raisonnement. On peut former un rectangle BGFE comme illustré ci-contre. Ainsi, pour déterminer l’aire du triangle DBC, on peut déterminer l’aire du rectangle BGFE et soustraire l’aire des trois triangles rectangles qui entourent le triangle DBC. Ces trois triangles sont illustrés en couleur.
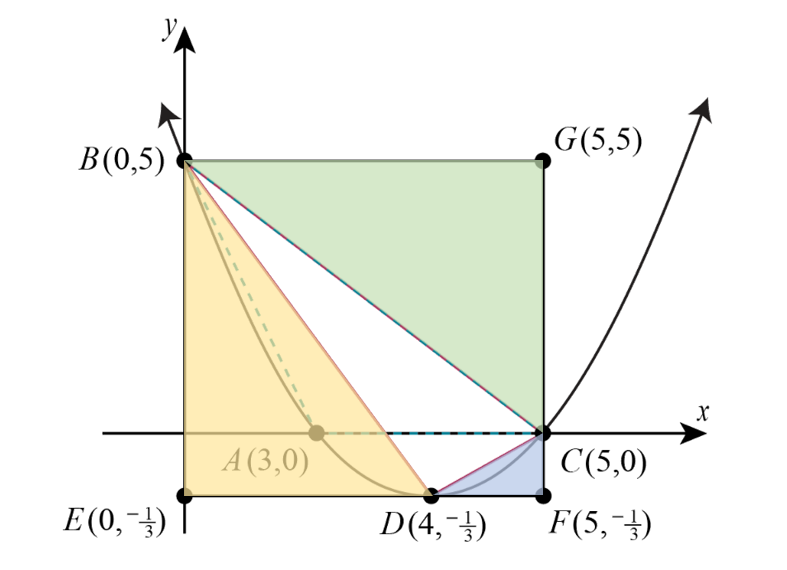
Calculons l’aire des triangles jaune, vert et bleu :
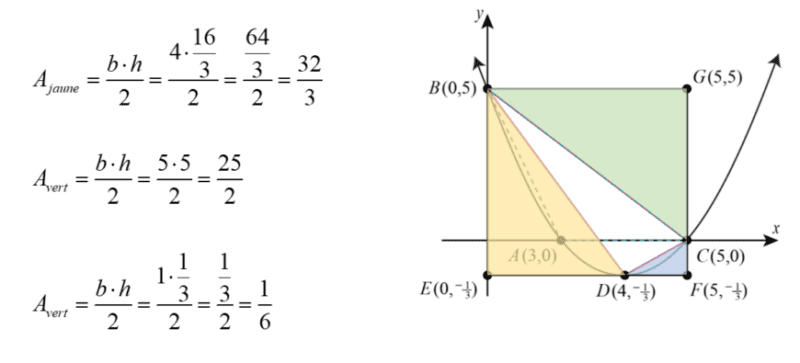
Il ne reste qu’à déterminer l’aire du rectangle BGFE et de lui soustraire la somme de l’aire des trois triangles.
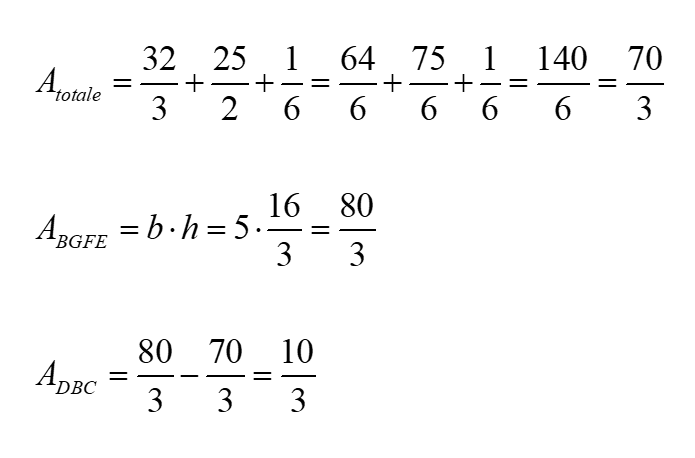
3e raisonnement possible
Une fois que le sommet de la parabole est identifié, il est également possible d’utiliser ce raisonnement. On peut séparer le triangle DBC en deux triangles distincts BPC et PCD.
En déterminant les coordonnées de P, nous pourrons ensuite déterminer l’aire de chacun des deux triangles.
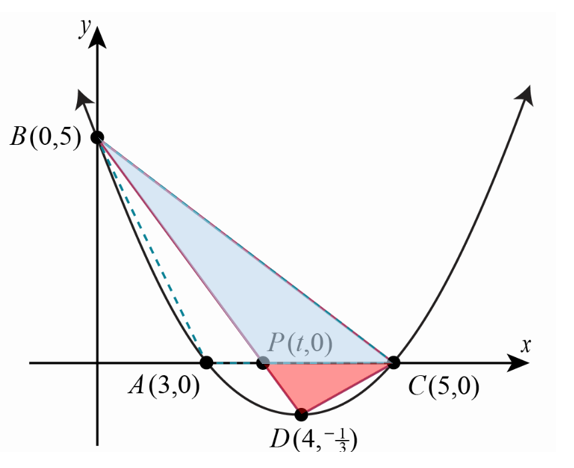
On peut déterminer la pente de la droite BD et son équation.

Avec l’équation, nous pouvons ensuite déterminer l’abscisse du point P, ce qui nous permettra de déterminer la mesure du segment PC.
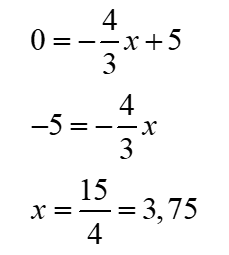
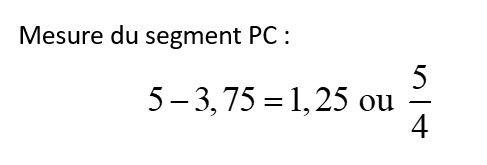
Il ne reste qu’à calculer l’aire des triangles bleu et rouge et à en faire la somme.
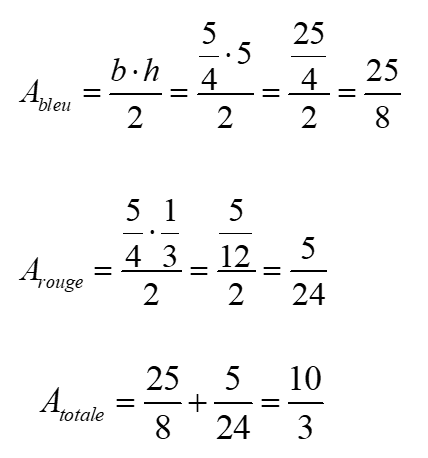
Voici un lien vers un graphique dans DESMOS qui pourrait vous soutenir pour la présentation du problème et/ou de sa solution.
Ressources
Lien vers le diaporama contenant l’ensemble des images de cet article (privilégier Microsoft Powerpoint pour que tout fonctionnent correctement).
Lien vers la tâche originale et le corrigé du CEMC.
N’hésitez pas à m’écrire si vous avez des questions ou des commentaires! Je suis également très intéressé à recevoir vos exemples de raisonnements ou des traces des raisonnements de vos élèves. Il me fera plaisir d’ajouter d’autres exemples de raisonnements à cet article!
martin.roy005@csssamares.gouv.qc.ca
Dernière mise à jour de cet article : 6 mai 2025
Une ressource très riche en problèmes!
Chaque semaine, le CENTRE d’ÉDUCATION en MATHÉMATIQUES et en INFORMATIQUE de l’Université de Waterloo partage de riches problèmes (pour la 3e à la 12e année). Les solutions de chacun de ces problèmes sont partagées une semaine plus tard.
Lien pour avoir accès aux problèmes en français
Lien pour avoir accès aux problèmes en anglais (vous aurez ainsi accès aux problèmes 11e/12e année)
Archives des problèmes des années 2022-2023 et 2023-2024
Les archives contiennent également l’ensemble des solutions des problèmes!