Une de vos collègues m’a récemment questionné par rapport à l’écriture des rapports en 2e secondaire (avec les deux points “:” ou avec la barre de fraction) et une certaine incohérence avec ce qui est proposé/enseigné en 4e secondaire quand il est question de point de partage d’un segment.
En résumé, sa question était la suivante : pourquoi un rapport 3 : 4 s’exprime aussi 3/4 en 2e secondaire alors qu’en 4e secondaire avec le point de partage, un rapport partie à partie de 3 : 4 s’exprimera 3/7 en fraction?
J’ai réfléchi à la question et consulté certains ouvrages, en plus de m’entretenir avec certaines personnes à ce sujet. Je vous résume l’essentiel de ce que j’en ai tiré.
Je suis allé voir certaines définitions de ce qu’est une proportion. J’avais entre autres observé dans un cahier d’activités édité au Québec la définition suivante : Une proportion est une égalité entre deux rapports. Je me suis posé la question à savoir si on doit plutôt dire qu’une proportion est une égalité entre deux rapports ou entre deux taux puisque selon moi, une proportion couvre beaucoup plus large qu’uniquement les rapports. Certains privilégient une définition comme celle-ci : une proportion est une équivalence entre deux ratios. Le mot équivalence fait référence au fait qu’on observe la même relation entre chacune des paires de quantités comparées. Bref, on peut même dire qu’on met en relation… deux relations!
On peut dire par exemple qu’il y a une équivalence entre les deux ratios suivants :
- il y a 8 filles et 12 garçons dans un groupe d’élèves;
- il y a 20 assiettes et 30 bols dans une armoire.
On peut alors établir la proportion suivante :
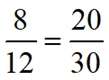
À noter que dans son article Le symbolisme en question – Les proportions (Revue Envol, 2022), M. Proulx utilise davantage l’expression ratio, puisque la distinction entre un rapport et un taux (bien que ce soit dans le programme et la PDA), n’est pas un élément clé du raisonnement proportionnel. En s’attardant à la relation entre deux quantités, cette préoccupation par rapport à la nature des quantités et le nom à leur attribuer est secondaire.
Maintenant, si on s’attarde plus spécifiquement à la notation d’un ratio, l’écriture avec les deux points est souvent une écriture privilégiée en 2e secondaire. C’est une écriture qui longtemps a permis de distinguer les fractions des ratios. Cependant, l’élève sera exposé à des ratios exprimés avec l’écriture fractionnaire pendant son parcours scolaire; exposer les élèves à cette notation s’avère donc nécessaire.
Par exemple, s’il y a 3 conifères et 4 feuillus sur un terrain, on peut dire que le ratio entre les conifères et les feuillus est de 3 : 4. On peut aussi inverser le ratio et dire qu’entre les feuillus et les conifères, le ratio est de 4 : 3. Finalement, on peut s’attarder au ratio entre le nombre de feuillus et le nombre d’arbres au total sur le terrain; on a alors le ratio 4 : 7. Dans tous les cas, c’est le contexte qui nous permet de bien interpréter ou de bien écrire le ratio en question.
Tel que souligné, on peut également utiliser l’écriture fractionnaire pour représenter un ratio. Les ratios ci-dessus pourraient alors être exprimés avec 3/4, 4/3 et 4/7. Encore ici, le contexte donné nous permet de bien comprendre la nature du ratio exprimé. Un ratio exprimé avec la notation fractionnaire ou avec les deux points “:” sans aucun contexte ne nous permet pas beaucoup d’interpréter la situation en question.
Avec les fonctions, on utilise l’écriture fractionnaire pour exprimer le ratio entre deux quantités. Cela devient beaucoup plus “pratique” puisqu’on peut ensuite utiliser la puissance de l’écriture fractionnaire pour effectuer des opérations. Mais en réalité, c’est le ratio entre deux quantités qui est exprimé (et non un seul nombre). Ainsi, une pente de ¾ représente un déplacement de 3 en y pour un déplacement de 4 en x. Voici donc un exemple où l’écriture fractionnaire est privilégiée pour exprimer un ratio.
Autre point que je trouvais fort intéressant à vous partager. Par convention, on ne peut pas vraiment écrire une fraction en utilisant des « nombres décimaux ». Par exemple : 1,5/2. Cependant, on peut très bien exprimer un ratio en utilisant des nombres décimaux puisqu’on exprime alors une relation entre deux quantités. Par exemple, pour chaque 100 km effectués en voiture, celle-ci consomme 8,9 litres. On pourrait exprimer ce ratio ainsi : 8,9/100. Et il n’y aurait pas de problème au plan mathématique, puisqu’on exprime alors une relation entre deux quantités et non pas, par exemple, un nombre rationnel ou une fraction-partie-d’un-tout.
Maintenant, parlons du point de partage en 4e secondaire. On enseigne aux élèves qu’un rapport “partie à partie” de 4 : 3 peut s’écrire 4/7 puisqu’on considère alors que lorsque c’est exprimé avec la barre de fraction c’est un rapport “partie à tout”. Et c’est là que ça devient possiblement incohérent avec ce qu’on enseigne en 2e secondaire. En fait, c’est le passage de 4 : 3 à 4/7 qui est mathématiquement discutable. Nous avons des habitudes dans notre programme de mathématiques au Québec, mais à la vue de ce qui a été dit plus haut, celles-ci ne sont pas nécessairement alignées d’une année scolaire à l’autre. Cela étant dit, on doit faire avec et seulement être conscient que c’est spécifiquement dans le contexte du point de partage qu’un rapport 4 : 3 devient « tout à coup » 4/7 dans nos façons de faire.
Si des élèves de 4e secondaire remarquent cette différence avec ce qu’ils ont appris plus tôt dans leur parcours, vous pourrez alors les féliciter d’avoir déceler cette petite incohérence et leur dire que c’est spécifiquement dans le contexte du point de partage en 4e secondaire qu’on a cette particularité.
En conclusion, en mathématiques, il faut parfois accepter et tolérer certaines ambiguïtés (comme celles-ci entre fraction, ratio, écriture, point de partage). Il semble important de toujours considérer la “lunette” avec laquelle on analyse et traite la situation, et être conscient qu’avec une autre “lunette” on pourrait avoir une autre lecture!
Pour aller plus loin, je vous recommande cet excellent article de Jérôme Proulx (revue Envol 2022).