À quoi ça sert le rang centile? Quelle formule privilégier pour le rang centile? Est-ce que le Ministère demande à ce qu’on enseigne une formule en particulier? Quelques pistes de réponse dans cet article.
Le rang centile est la mesure de position d’une donnée dans une série statistique ordonnée et divisée en 100 intervalles de même effectif.
Exemple : Lorsqu’on dit que le rang centile d’un élève est 92, cela signifie qu’il y a 1% des élèves de son groupe qui ont le même rang que lui, que 91% des élèves de ce groupe sont dans des intervalles inférieurs au sien et que 8% des élèves de son groupe sont dans des groupes supérieurs au sien.

Lexique mathématique : enseignement secondaire (de Champlain, Mathieu, Patenaude, Tessier)
Deux formules sont généralement proposées/enseignées aux élèves :

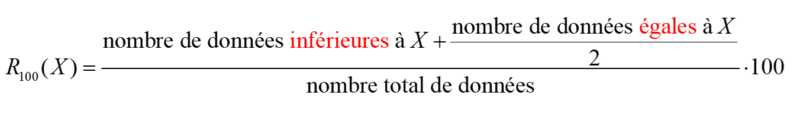
La seconde formule pourrait également être présentée ainsi :
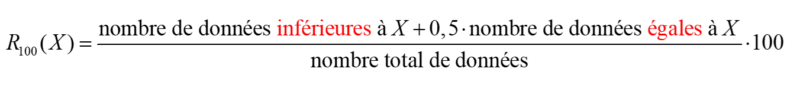
Quelle formule privilégier?
Ayant posé la question dans le passé aux personnes responsables des programmes de maths au Ministère, la réponse courte est que c’est à nous de faire un choix. Il existe plusieurs définitions/formules pour le rang centile. Il serait intéressant de faire réfléchir les élèves sur les distinctions entre les formules et de les tester dans différentes situations. Dans quelles situations une formule pourrait être plus avantageuse ou pertinente qu’une autre?
Par exemple, voici une distribution de données :
1 – 2 – 2 – 3 – 4 – 5 – 6 – 7 – 8 – 9 – 9 – 9 – 9 – 9 – 9 – 9 – 9 – 11 – 12 – 13 – 16 – 18 – 20
Si on calcule le rang centile de « 9 » à l’aide des deux formules, voici les résultats obtenus :
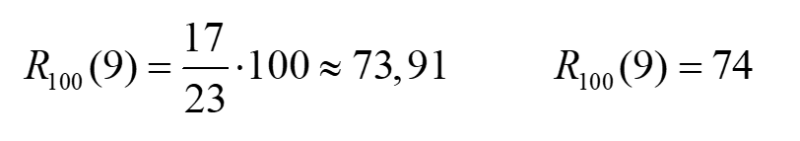
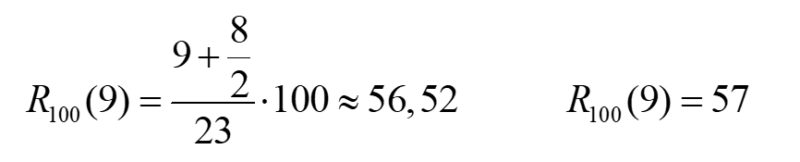
Cela donne deux résultats très différents, pourtant on s’intéresse aux mêmes données de la distribution.
Si on calcule le rang centile des données 8 et 11, situées de part et d’autres des données 9 qui se répètent, voici les résultats obtenus :

On peut alors constater que le résultat obtenu avec la deuxième formule pour le rang centile de « 9 » (57) est beaucoup plus représentatif de l’endroit où se situent les données « 9 » dans la distribution. 57 est davantage au centre de 40 et 79 par rapport au 74 qui « tirent » beaucoup les données vers le haut…
La seconde formule permet donc d’avoir un résultat plus représentatif pour cette mesure de position dans la distribution.
Et dans l’épreuve ministérielle?
Rassurez-vous puisque peu importe la formule utilisée parmi celles ci-dessus dans l’épreuve ministérielle, le résultat sera la même. Ceux qui élaborent les épreuves prennent cela en considération.
Si on demande aux élèves de déterminer le rang centile d’une donnée dans les sections A ou B de l’épreuve ministérielle (choix multiples ou réponses courtes), le résultat sera EXACTEMENT le même peu importe la formule utilisée.
Advenant qu’on ait à utiliser ce concept dans la section C, la formule utilisée n’influencera pas non plus le résultat final de l’élève. Dans une épreuve antérieure, le Ministère a utilisé la formule avec la division par 2 dans un exemple de raisonnement du guide de correction (section C). Dans le problème, les élèves devaient vérifier si le rang centile associé à un résultat était supérieur à 90. En utilisant la première formule, ils obtenaient 89 et avec la seconde, ils obtenaient 88. Ça ne changeait donc pas la conclusion de l’élève à la fin de ce numéro.
Important
Il s’avère important de mentionner aux élèves que cette mesure statistique est pertinente pour de grandes distributions de données. Il n’y a pas de nombre absolu de données à partir duquel le rang centile devient pertinent, mais un nombre trop petit de données rend la mesure très volatile. Plus il y a de données, plus la pertinence du rang centile sera élevée.
Pour de plus petits groupes, d’autres mesures seraient plus appropriées notamment le rang cinquième (qui n’est pas au programme). Ultimement, je dirais qu’aucune mesure de position en particulier n’est requise quand on est capable de visualiser et d’apprécier la position d’une donnée “à l’oeil”!
C’est important à considérer puisque plusieurs cahiers d’activités proposent des exerciseurs sur le rang centile avec des distributions très (trop) petites. Ça peut être intéressant pour comprendre le concept, mais on doit s’éloigner de ces petites distributions pour que ce soit plus approprié.
*À noter que je suis tout à fait conscient que les exemples que j’ai présentés plus haut contiennent très peu de données. N’hésitez pas à me faire parvenir des exemples plus pertinents; je me ferai un plaisir d’ajuster mon article!😉
En résumé
La formule :

est plus simple à comprendre. Pour trouver la position de la donnée à partir du rang centile, l’élève peut voir qu’on part de la même formule et qu’on applique un raisonnement algébrique.
Cette formule répond à la question : « Quel pourcentage des élèves a obtenu une note inférieure ou égale à la mienne ? » Bien qu’elle soit plus simple et facile à comprendre, elle est statistiquement moins précise.
La formule :
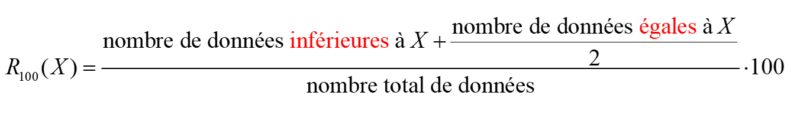
permet d’être plus “juste” ou « équitable » pour les résultats égaux. Elle permet de situer les résultats égaux “au milieu” de ceux-ci et non pas à l’extrémité supérieure. Également, elle permet d’éviter d’avoir plusieurs résultats avec un rang centile de 100 lorsque plusieurs résultats sont ex aequo au sommet. Par exemple, un élève avec le résultat le plus élevé à un examen mais qui partage cette position avec plusieurs autres élèves aura un rang centile comme 98 ou 99, mais pas 100.
N’hésitez pas à m’écrire si vous avez des questions ou des commentaires en lien avec cet article : martin.roy005@csssamares.gouv.qc.ca.
Je vous laisse ici un diaporama que j’ai utilisé en classe dans la précédente décennie si ça peut vous être utile!
Références :
De Champlain, D., Mathieu, P., Patenaude, P. et Tessier, H., Lexique mathématique, enseignement secondaire, 2e édition, 1996, Les Éditions du Triangle d’Or, distribution Modulo Éditeur, téléphone : (514) 738-9818, Ligne sans frais : 1-888-738-9818.

