Un problème qui nécessite qui nécessite de mobiliser ses connaissances sur le cercle et une bonne dose de réflexion! Un problème accessible pour les élèves de 2e secondaire.
D’autres problèmes similaires pour les élèves de 3e, 4e et 5e secondaire sont également proposés : Le territoire de Fiona et Le bélier.
Pour plus de détails, c’est par ici ⬇️.
Catherine a accepté de tondre la pelouse à l’aide de la tondeuse électrique. La maison est de forme rectangulaire. Sa longueur est de 15 mètres et la largeur, de 10 mètres. À deux mètres du coin de la maison, il y a une prise électrique qui lui permet de brancher sa tondeuse. Le fil de la tondeuse mesure 20 mètres.
Quelle est l’aire maximale que Catherine peut tondre?
D’emblée, mettons quelque chose au clair! Je suis d’accord avec vous qu’une tondeuse électrique avec un fil, ça fait « années 80 », mais j’ai repris le problème tel quel! 🤪 Si vous avez une idée pour conserver l’esprit de la tâche tout en mettant un contexte plus contemporain, merci de m’écrire! J’ajouterai vos idées à cet article avec plaisir! 😉
Il est d’abord assez évident qu’on peut tondre le demi-disque illustré ci-dessous. Ce demi-disque a un rayon de 20 mètres étant donné que le fil électrique a une longueur de 20 mètres.
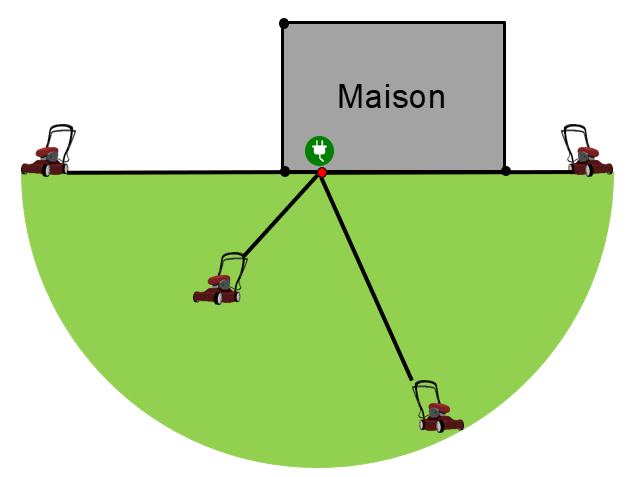
À partir du coin gauche de la maison, ce sera le centre d’un nouveau cercle (ou plutôt quart de cercle) que l’on peut tondre qui aura un rayon de 18 mètres (20 mètres de fil moins les 2 mètres qui séparent le coin de la maison à la prise).
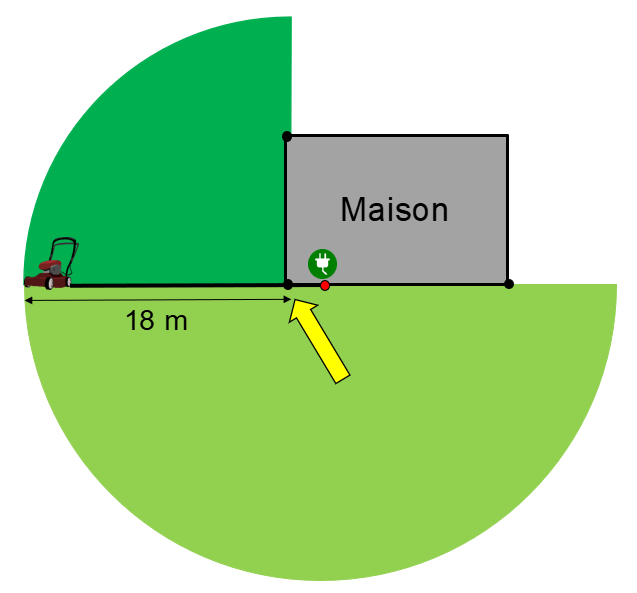
À partir du coin en haut à gauche de la maison, ce sera le centre d’un nouveau quart de cercle que l’on peut tondre qui aura un rayon de 8 mètres (20 mètres de fil moins les 2 mètres qui séparent l’autre coin de la maison à la prise moins la largeur de la maison).
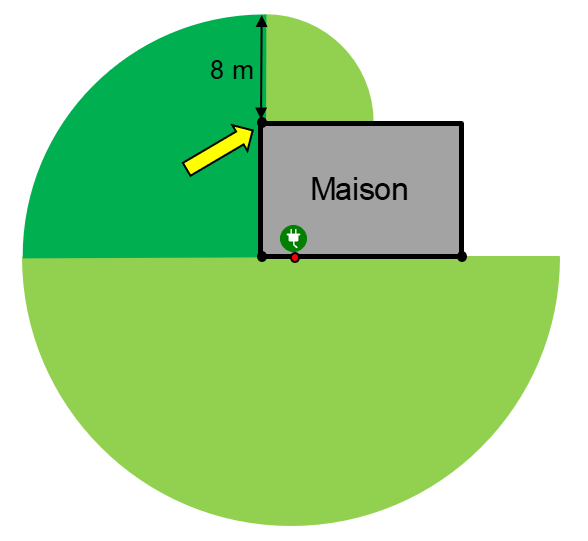
Finalement, il ne faut pas oublier le bout à droite de la maison. À partir du coin en bas à droite de la maison, Catherine pourra tondre un autre quart de cercle qui aura un rayon de 7 m (20 mètres de fil moins les 13 mètres qui séparent ce coin de la maison à la prise électrique.
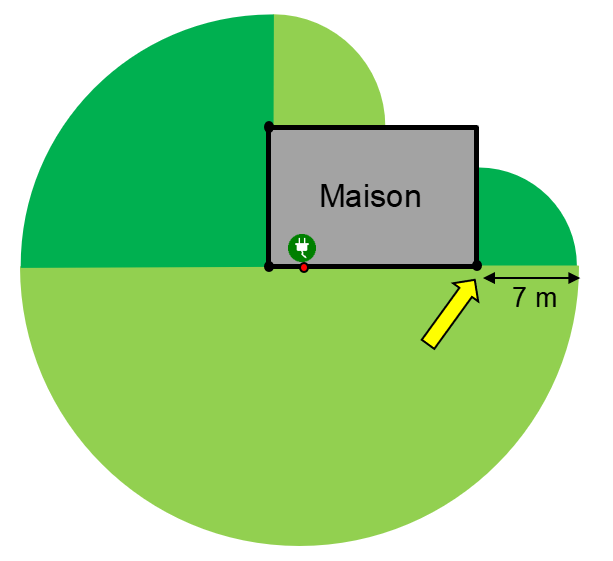
Il ne reste plus qu’à effectuer les calculs pour déterminer l’aire de chaque section puis à additionner le tout. Voici l’aire de chacune des sections :
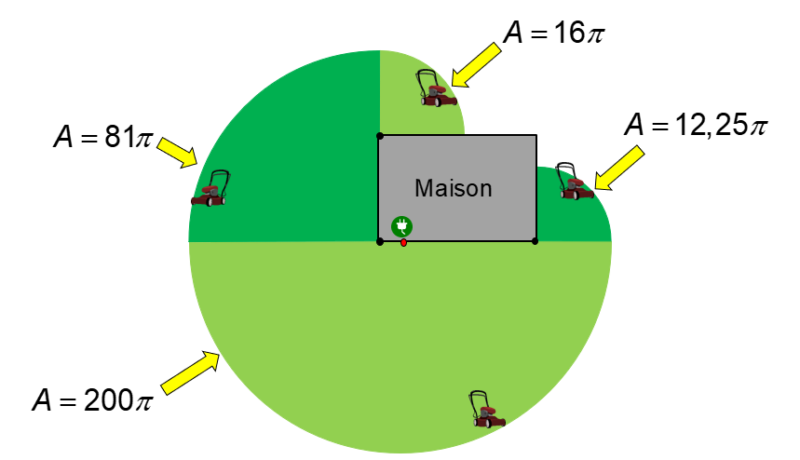
Un grand total de (309,25π) m2 ou environ 971,54 m2.
Lien vers un diaporama qui contient une bonne partie des images présentées dans cet article. (privilégier Microsoft Powerpoint).
Ce problème faisait partie du concours Optimath en 2021.
Le territoire de Fiona
Voici un problème similaire à celui de la tondeuse, mais qui nécessitera des concepts de niveau 3e secondaire ou de 4e secondaire.
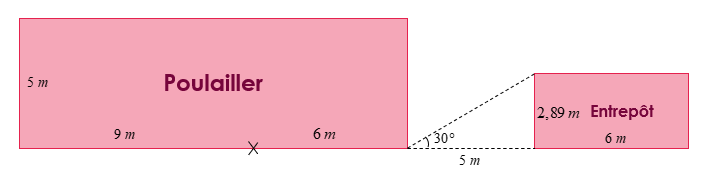
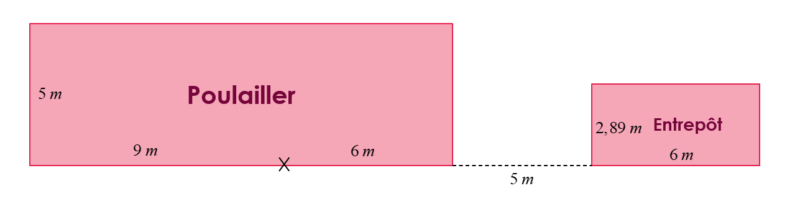
Valérie possède un poulailler et aimerait faire fuir les renards qui rôdent autour. Le mois dernier, elle s’est acheté une chienne appelée Fiona. Le poulailler est clôturé sur un terrain rectangulaire mesurant 15 m sur 5 m. De plus, un petit entrepôt dont les dimensions sont indiquées sur la figure est situé à 5 mètres du poulailler*.
Valérie attache Fiona à l’extérieur de la clôture à un poteau illustré par un X sur le plan ci-dessus. La
chienne peut donc circuler librement sur le reste du terrain.
Sachant que la corde de Fiona mesure 14 m, détermine l’aire du terrain que Fiona peut couvrir.
*Si jamais un élève pose la question, les façades des deux bâtiments sont parfaitement alignées.
Un peu comme le problème précédent avec la tondeuse, on peut réussir à illustrer l’espace que Fiona pourra couvrir de cette façon :
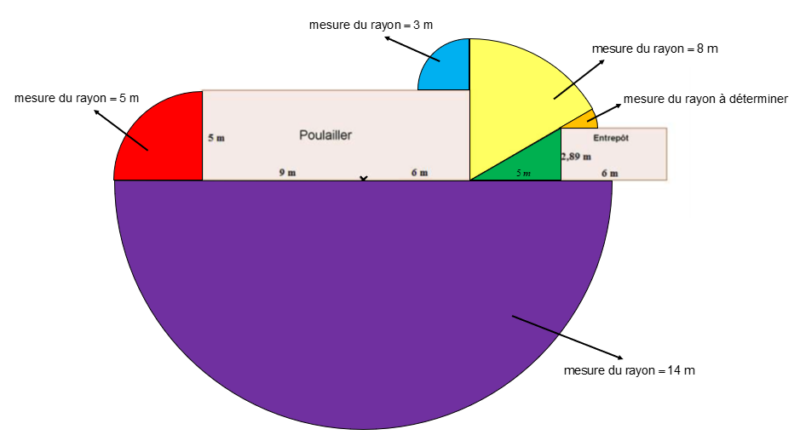
Il ne restera qu’à calculer l’aire de chacune de ces sections et le tour est joué! Avant de déterminer l’aire de chacune des sections, voici la stratégie utilisée pour déterminer le rayon de chacun des secteurs de cercle. La stratégie sera illustrée pour le quart de cercle bleu, mais la même logique s’applique pour les autres secteurs (rouge, jaune et orange).
Le chemin le plus court pour se rendre au coin en haut à droite du poulailler est illustré par les deux traits rouges. Il y a donc 11 mètres pour arriver à ce coin (6 + 5). La corde ayant une longueur totale de 14 mètres, il reste donc 3 mètres de rayon à Fiona pour se déplacer à partir de ce point qui devient le centre du quart de cercle bleu.
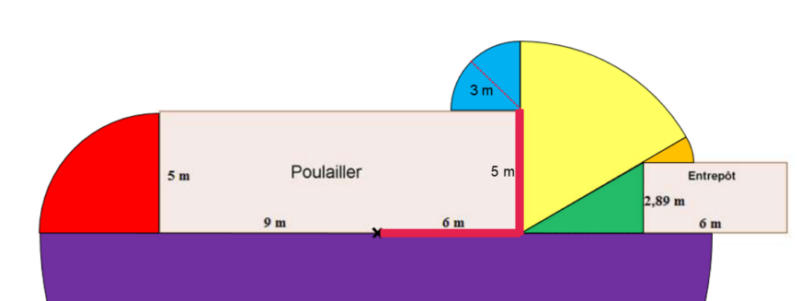
De la même façon, nous pouvons déterminer que le rayon du du secteur rouge est de 5 mètres et que le rayon du secteur jaune est de 8 mètres. Calculons maintenant l’aire de chacune des sections!
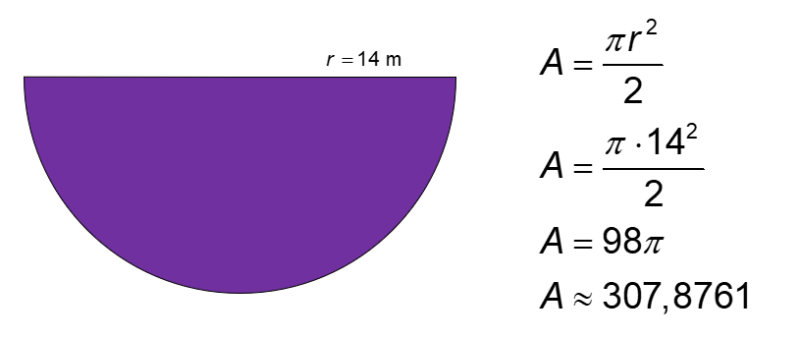
Aire de la section mauve.
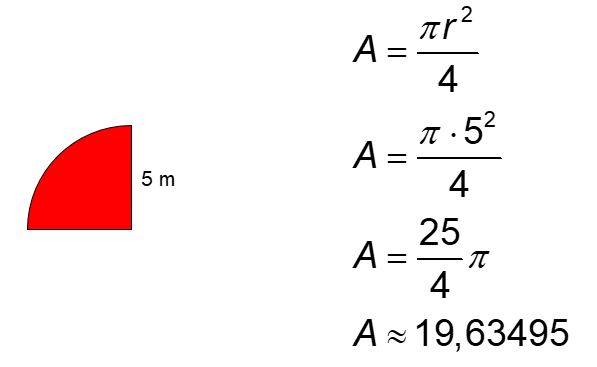
Aire de la section rouge.
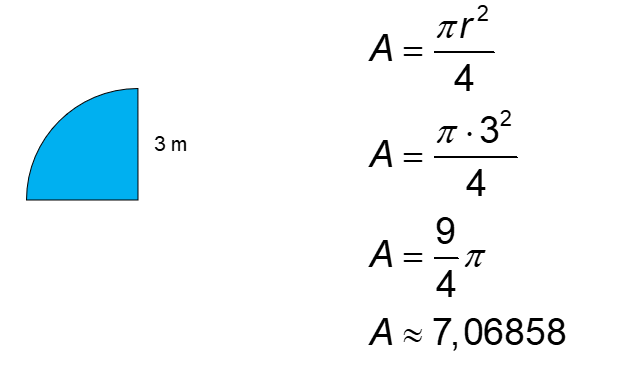
Aire de la section bleue
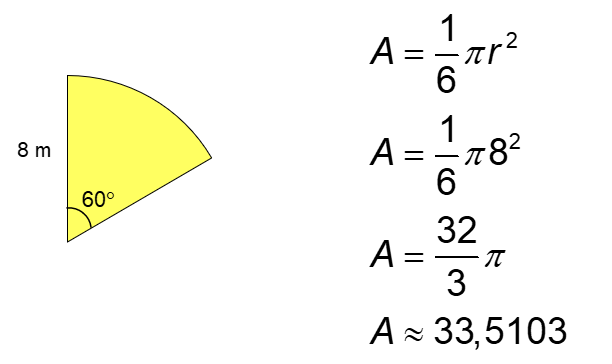
Aire de la section jaune.
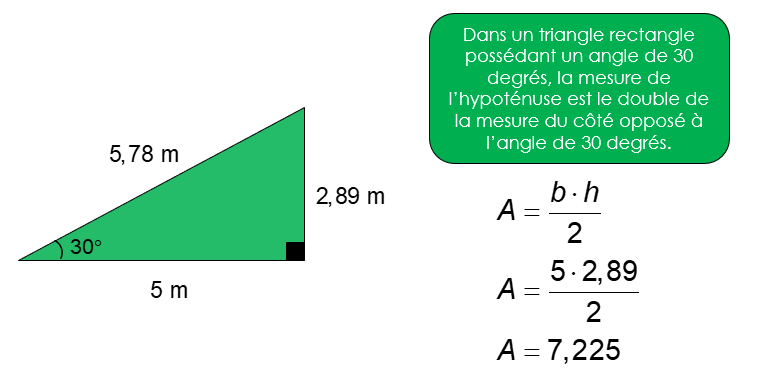
Aire de la section verte. Pythagore aurait également pu être utilisé pour déterminer la mesure de l’hypoténuse. Cette mesure n’est pas essentielle pour déterminer l’aire de la section verte, mais elle sera nécessaire pour savoir quelle est la mesure du rayon du secteur de cercle orange.
Aire de la section orange.
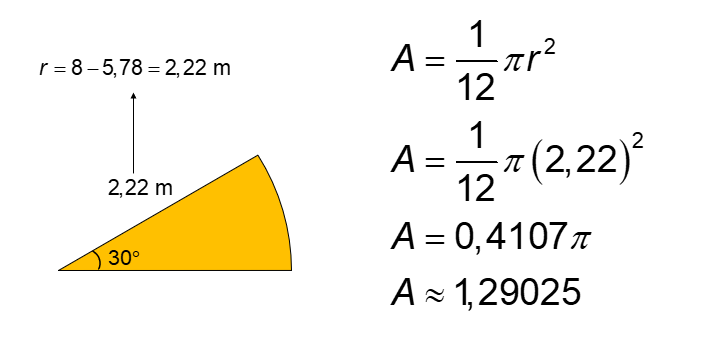
La somme des six sections est donc égale à environ 376,6051 m2.
Lien vers un diaporama qui contient une bonne partie des images présentées dans cet article. (privilégier Microsoft Powerpoint). Au besoin, je pourrai vous faire parvenir une version PDF.
Ce problème faisait partie du concours Optimath+ en 2021.
Pour augmenter légèrement le niveau de difficulté du problème, vous pourriez donner cette image au départ plutôt que celle qui indique l’angle de 30 degrés.
Le bélier – Un problème pour experts!

Ce dernier problème vous demandera davantage de réflexion et de créativité. Néanmoins, il se résout à l’aide de concepts de niveau 4e secondaire.
Un jeune bélier est un peu trop vagabond. Il est donc attaché à l’un des coins d’une bergerie de forme carrée qui mesure 10 mètres de côté. Il est donc limité dans ses déplacements. Sa corde mesure 22 m.
Déterminez la surface d’herbe que le bélier peut brouter. Source : Facebook
Pour ce problème, je vous laisse seulement la réponse : environ 1362,7917 m2. Si vous désirez obtenir une solution détaillée, vous devrez me faire parvenir les différentes étapes de votre raisonnement! Bien hâte de voir vos démarches! 😉
N’hésitez pas à m’écrire si vous avez des questions, des commentaires ou si vous souhaitez partager votre expérience après avoir utilisé ce problème avec vos élèves.
martin.roy005@csssamares.gouv.qc.ca
Dernière mise à jour de cet article : 16 décembre 2024

