Réciproque

Un concept parfois mal-aimé en mathématique est celui de la réciproque. L’objectif de cet article est de donner quelques pistes afin de rendre ce concept plus significatif pour les élèves. 

Une situation peut être vue sous différents angles. Lorsqu’on parle de variable dépendante et indépendante, c’est le moment parfait pour parler du concept de réciproque avec nos élèves. Par exemple, la quantité de calories dépensées et le nombre de km parcourus lors d’une course à pied. On peut voir la situation en se disant que plus je parcours une longue distance, plus mon nombre de calories dépensées sera élevé. Les calories dépendent alors du nombre de kilomètres parcourus. Sous cet angle, nous avons le nombre de km comme variable indépendante et le nombre de calories comme variable dépendante. Par contre, si on se questionne à savoir quelle distance devrait être parcourue pour dépenser un certain nombre de calories, la distance devient alors la variable dépendante et le nombre de calories, la variable indépendante. Cette deuxième situation correspond à la réciproque de la situation initiale. Si on représentait ces deux situations dans deux graphiques, ceux-ci contiendraient les mêmes informations, mais présentées sous deux angles différents. On pourrait tout de même interpréter le graphique et répondre aux mêmes questions.

Pour que la notion de réciproque ait du sens pour nos élèves, on doit la rattacher à des situations contextualisées, car simplement intervertir les x et les y ne veut pas dire grand chose lorsque le graphique n’est rattaché à aucun contexte. Une définition purement mathématique de la réciproque rendra ce concept très (trop) abstrait pour les élèves. Par exemple, voici la définition sur Allô Prof ci-dessous : la définition est juste, mais elle est beaucoup trop abstraite pour un élève particulièrement en 3e secondaire. En ajoutant les deux graphiques ou les deux tables de valeurs d’une fonction et de se réciproque qui sont contextualisées, cela aidera énormément à comprendre.

Prenons une autre situation. Pour pouvoir faire des manèges à une fête foraine, il en coûte d’abord 3,00$ pour se procurer un bracelet (ou pour entrer sur le site peu importe) et il faudra ensuite débourser 2,00$ pour chaque tour de manège. Si on s’intéresse aux dépenses totales en fonction du nombre de tours de manèges effectués, on aurait donc comme fonction : 

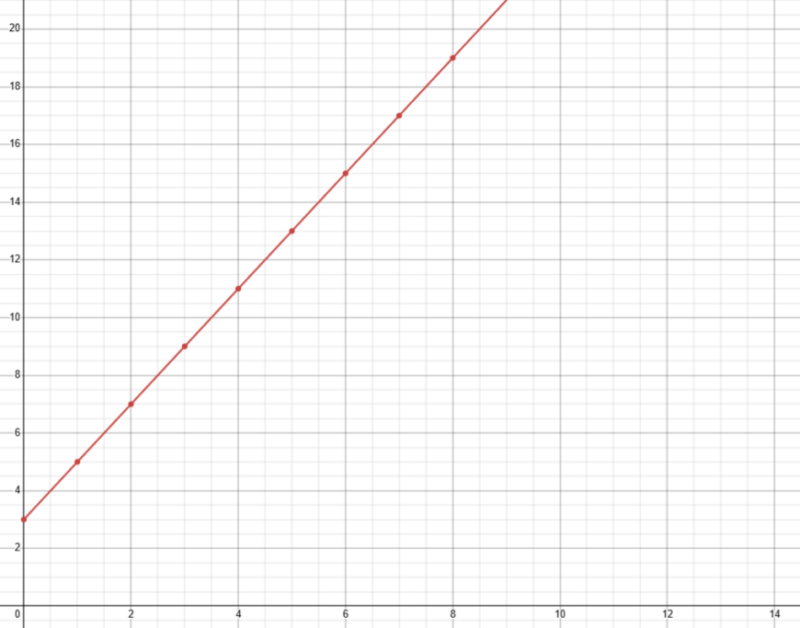
Le graphique associé à cette situation serait le suivant : 

 

Si on s’intéresse au nombre de de tours de manèges qu’il est possible d’effectuer selon la quantité d’argent que nous avons dans notre portefeuille, on voit alors la même situation sous un autre angle. Le nombre de tours de manèges devient alors dépendant de l’argent que nous avons dans notre portefeuille (ou d’une certaine somme qu’on voudrait dépenser). 

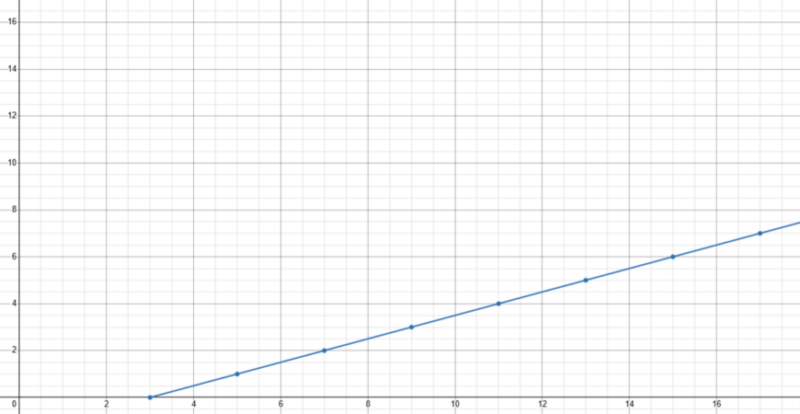
Le graphique associée à cette nouvelle fonction : 

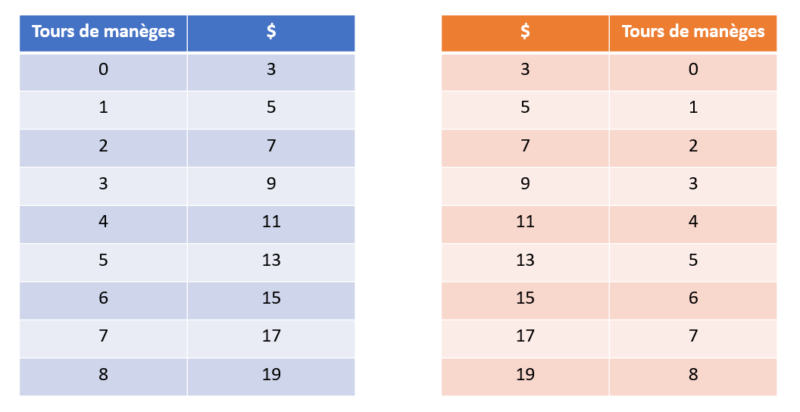
Et en regardant les deux tables de valeurs associées à ces deux situations, on peut alors très bien observer que les x et les y ont été intervertis :

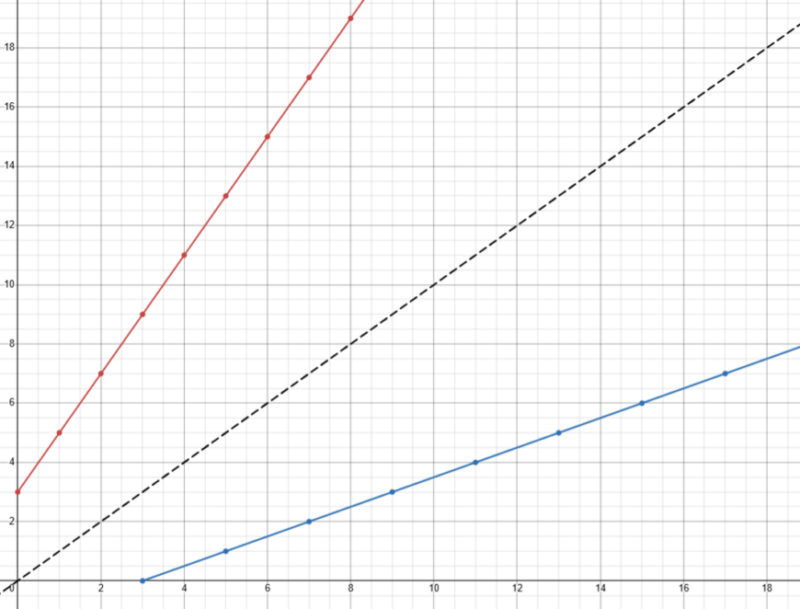
On peut également bien observer à partir des deux graphiques que les deux fonctions possèdent un axe de symétrie y=x représenté en pointillé ci-dessous : 

En contextualisant les situations, il devient alors plus concret et significatif d’intervertir les variables et de trouver une règle d’une nouvelle fonction qui est simplement une autre façon de voir la situation. Ainsi, il devient relativement simple d’introduire le concept de réciproque en 3^e secondaire. 

Mon exemple préféré est le suivant. On s’intéresse aux variables suivantes : la vitesse d’une voiture et la distance de freinage. On pourrait représenter cette situation en se disant qu’on cherche à connaître la distance de freinage d’une voiture selon la vitesse à laquelle elle roule. Sous cet angle, la variable indépendante serait la vitesse et la variable dépendante serait la distance. Par contre, lorsque les policiers procèdent à une enquête lors d’un accident, ils voient les liens entre ces variables sous un autre angle. Ils s’intéressent à la fonction réciproque : ils cherchent à savoir quelle était la vitesse de la voiture pour laquelle on connaît la distance de freinage. On pourrait à ce moment tracer le graphique en utilisant la distance comme variable indépendante et la vitesse comme variable dépendante. C’est exactement la même situation, mais vue sous deux angles différents.

Variables dépendante et indépendante

Maintenant, si on ne donne aux élèves que deux variables en leur demandant d’identifier la variable indépendante et la variable dépendante, il n’y a pas nécessairement de bonne ou de mauvaise réponse. On doit choisir sous quel angle on aborde le lien entre ces variables. Seulement l’ordre dans lequel on présentera les deux valeurs pourrait amener les élèves à voir la situation sous un angle ou sous un autre. Par contre si lorsqu’on présente les deux variables aux élèves, on établit d’emblée sous quel angle on souhaite que la situation soit analysée avec soit une table de valeurs, un graphique ou des mots clés comme “varie en fonction de” ou “selon”, il y aurait effectivement une seule bonne réponse. Je ne crois pas cependant que ce soit à ce niveau qu’on doit mettre beaucoup d’emphase. 

Différents exemples :

La quantité d’essence dans une voiture (en litres) et la distance à parcourir (en km).

On peut voir la situation en se disant que plus je mets de l’essence dans mon auto, plus je serai en mesure de parcourir une grande distance. Sous cet angle, nous avons la quantité d’essence comme variable indépendante et la distance en variable dépendante. Par contre, si on se questionne à savoir quelle quantité d’essence dans mon auto est nécessaire pour parcourir une certaine distance, la distance devient la variable indépendante et la quantité d’essence, la variable dépendante (puisque c’est la distance à parcourir qui influencera la quantité d’essence consommée).

Le nombre de points obtenus dans un examen à choix multiples et le nombre de bonnes réponses.

On peut voir la situation en se disant que plus j’ai de bonnes réponses, plus mon nombre de points sera élevé. Mes points dépendent du nombre de bonnes réponses. Sous cet angle, nous avons le nombre de bonnes réponses comme variable indépendante et le nombre de points comme variable dépendante. On pourrait également se demander combien de bonnes réponses nous devons obtenir pour atteindre un certain nombre de points. Sous cet angle, le nombre de bonnes réponses dépendrait du nombre de points à atteindre. Cette autre façon de voir la situation est la réciproque de la fonction telle qu’interprétée initialement. 

D’autres idées que vous pourriez exploiter :

• le temps passé à écouter notre émission préférée à la télévision et le nombre d’épisodes visionnés;
• le temps écoulé et le nombre de tours de piste lors d’une course à pied;
• le coût total de la location et le nombre de jours de location;
• etc.

Quels sont vos exemples préférés pour enseigner le concept de réciproque?
Quelles sont vos meilleures stratégies ou activités que vous proposez à vos élèves sur ce concept?

N’hésitez pas à m’écrire si vous avez des questions, des commentaires : martin.roy005@csssamares.gouv.qc.ca.

Merci à Geneviève Pilon pour l’inspiration de cet article! 

Dernière mise à jour de cet article : 22 janvier 2025