Oui, un autre problème de billes pour travailler certains concepts en probabilités! Mais c’est un problème très intéressant! 😁
Plus de détails ici ⬇️.

Un jeu de hasard consiste à tirer successivement et sans remise deux billes d’un sac. Le sac contient 10 billes de la même grosseur : des rouges et des vertes.
À ce jeu, la probabilité que les deux billes tirées soient rouges est de 1/15.
Quelle est la probabilité de tirer deux billes de couleur différente?
Source : Jean-Michel Panet, Groupe Facebook Mathématiques 106 et 206 https://www.facebook.com/groups/1605696109739716/permalink/3080519735590672/
Voici un exemple de raisonnement approprié.
Compte tenu que c’est un tirage sans remise et qu’il y a 10 billes au total dans de sac, le calcul qui permettra de déterminer la probabilités que deux billes tirées soient rouges aura ce format :
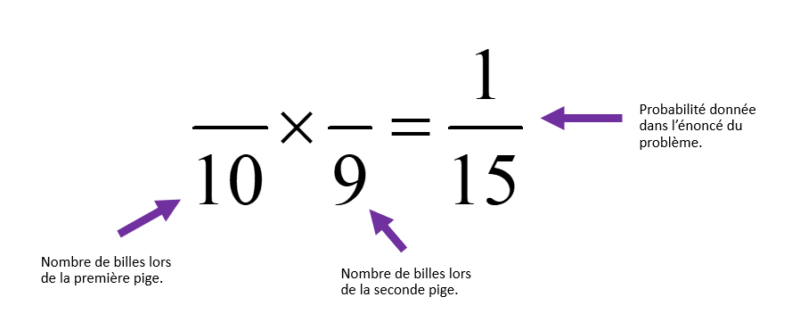
La multiplication des deux fractions de gauche ne donnera pas directement la fraction réduite 1/15. En multipliant les dénominateurs, on peut déduire que la fraction représentant le produit aura 90 comme dénominateur.
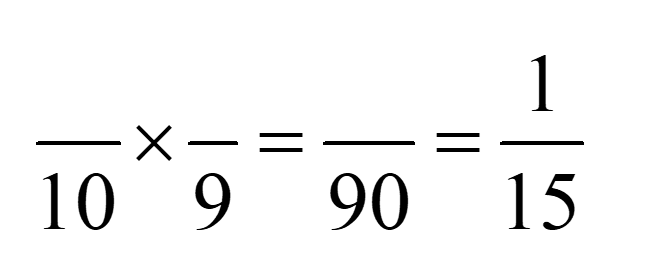
La fraction équivalente à 1/15 sera donc 6/90 :
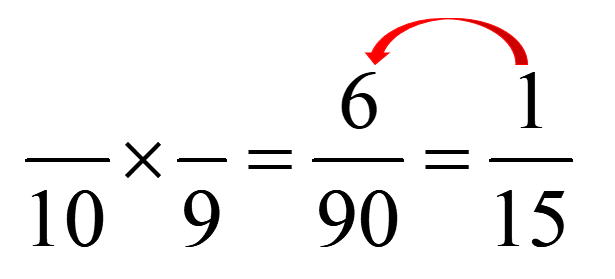
On doit donc déterminer quels nombres qui multipliés ensemble donneront 6. Considérant que ce sont deux billes rouges qui sont tirées une à la suite de l’autre sans remise, le deuxième nombre doit être 1 de moins que le premier.
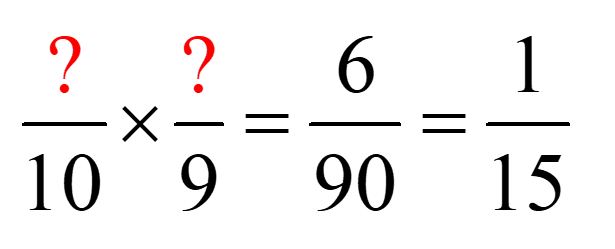
Il n’y a pas des tonnes de combinaisons possibles! On peut donc rapidement déterminer qu’il y a 3 billes rouges dans le sac. Ainsi, il y aura donc 7 billes vertes (il y a 10 billes au total).
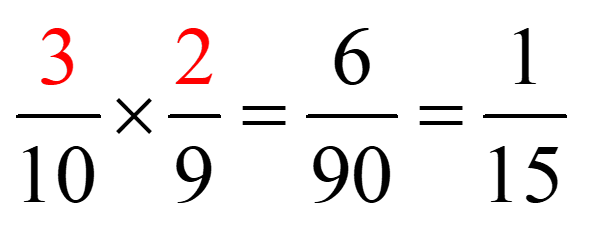
Pour répondre à la question, nous pouvons calculer la probabilité de tirer deux billes vertes. Ainsi en additionnant les probabilités de piger deux billes de la même couleur, nous pourrons trouver la réponse à question en utilisant le complément.
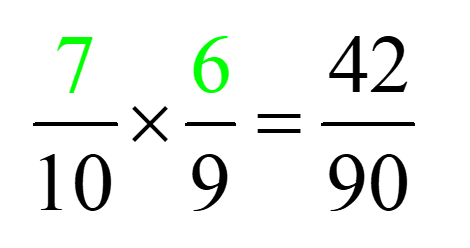
La probabilité de tirer deux billes de la même couleur :
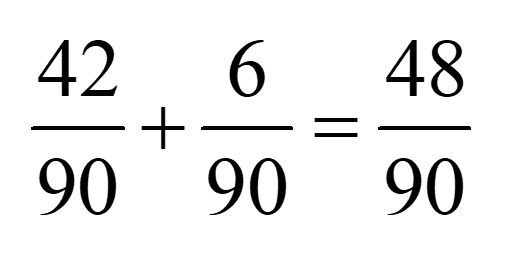
La probabilité de tirer deux billes de couleurs différentes :
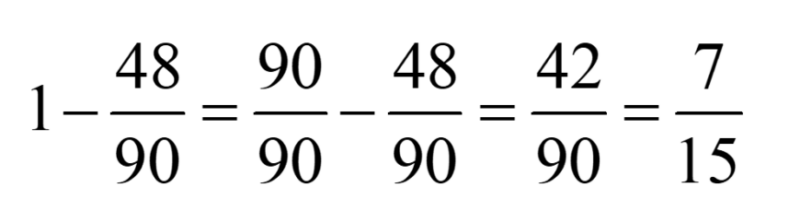
Lien vers le diaporama contenant l’ensemble de ces images (privilégier Microsoft Powerpoint pour que les animations fonctionnent correctement).
N’hésitez pas à m’écrire si vous avez des questions ou des commentaires! Je suis également très intéressé à recevoir vos exemples de raisonnements ou des traces des raisonnements de vos élèves. Il me fera plaisir d’ajouter d’autres exemples de raisonnements à cet article!
martin.roy005@csssamares.gouv.qc.ca
Dernière mise à jour de cet article : 19 novembre 2024

