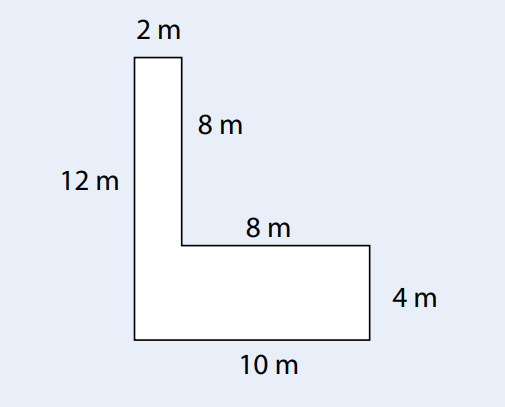
Combien de stratégies différentes êtes-vous en mesure d’identifier pour déterminer l’aire de cette figure? Deux? Trois? Quatre? Davantage? Ce problème est utilisé dans le Référentiel d’intervention en mathématique pour illustrer le concept de flexibilité. Il pourrait être utile pour vulgariser (et valoriser!) ce concept auprès de vos élèves.
Plusieurs exemples de stratégies dans cet article ⬇️.
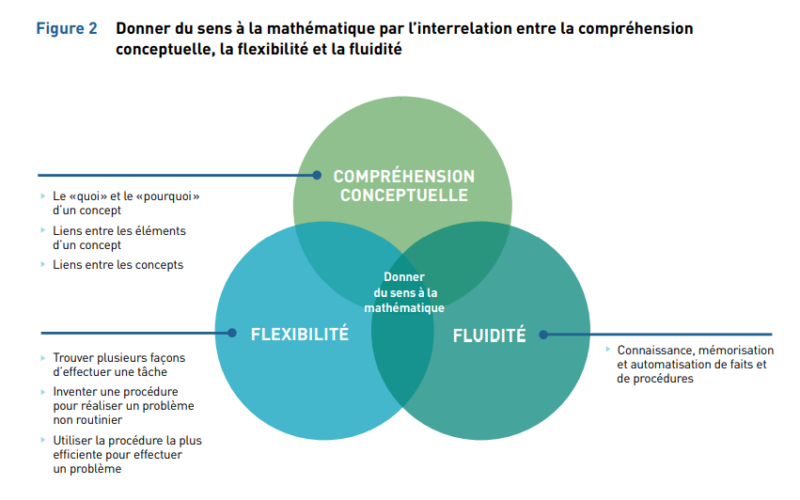
Flexibilité
Selon le Référentiel d’intervention en mathématique (page 8), la flexibilité fait référence au fait que l’élève connaisse plusieurs façons d’effectuer une tâche (Arslan et Yazgan, 2015; Kilpatrick, Swafford et Findell, 2001; MELS, 2009; MELS, 2010; Rittle-Johnson et Star, 2007; Star et Seifert, 2006).

Toujours dans ce même référentiel (page 9), on mentionne que pour plusieurs auteurs, le fait de connaître plusieurs façons d’effectuer une tâche n’est pas suffisant pour définir la flexibilité. Par exemple, Star et Seifert (2006, p. 283, traduction libre) mentionnent ce qui suit :

Le schéma qui suit présente les liens entre la compréhension conceptuelle, la flexibilité et la fluidité.
L’enseignant de mathématique devrait d’abord miser sur le développement de la compréhension conceptuelle pour que cette dernière assure une base solide pour le développement de la flexibilité et de la fluidité.
Voici maintenant quelques stratégies pour déterminer l’aire de cette figure.
1re stratégie : découper (horizontalement) la figure en 2 rectangles, calculer l’aire de chacun de ces rectangles puis en faire la somme.

2e stratégie : découper (verticalement) la figure en 2 rectangles, calculer l’aire de chacun de ces rectangles puis en faire la somme.

3e stratégie : compléter la figure pour former un grand rectangle, calculer l’aire totale de ce
rectangle puis soustraire l’aire du carré qui a été ajouté au coin supérieur droit.

4e stratégie : découper la figure en trois rectangles, déterminer l’aire de chacun de ces rectangles puis en faire la somme.

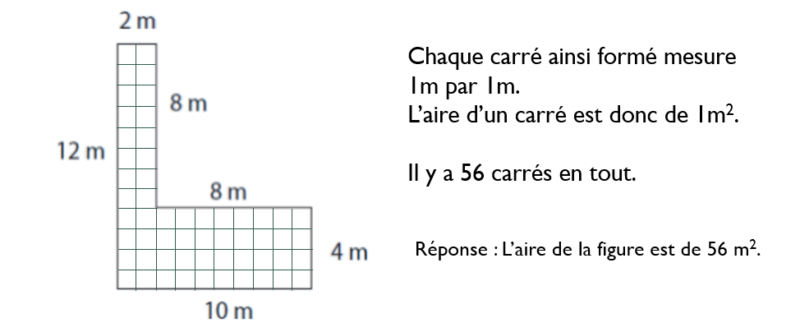
5e stratégie : découper la figure en plusieurs petits carrés de 1m par 1m.
6e stratégie : découper la figure en 2 trapèzes, calculer l’aire de chacun de ces trapèzes puis en faire la somme. Cette stratégie, bien qu’elle puisse paraître peu orthodoxe a été utilisée par un élève de 2e secondaire lors d’une de mes visites en classe. Je ne l’avais pas anticipé avant qu’il me la présente. Bien que ce ne soit pas nécessairement la stratégie la plus optimale pour résoudre ce problème, nous l’avons tout de même communiquée à l’ensemble de la classe. Le fait de voir différentes stratégies pour résoudre un même problème et de découvrir des raisonnements empruntés par nos pairs, qui sont plus éloignés de ceux que l’on emprunte habituellement, permet aux élèves de développer cette flexibilité et leur créativité lors de problèmes subséquents.

7e stratégie : En complément, ça pourrait être intéressant de déterminer une stratégie advenant qu’on donne au départ seulement ces mesures.
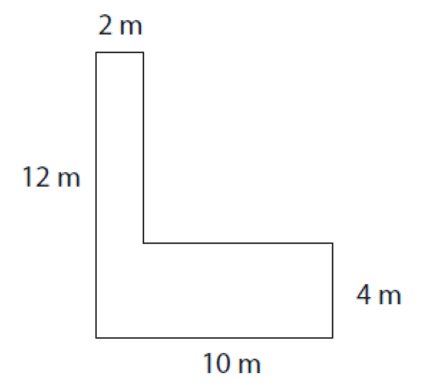
On pourrait évidemment déduire les mesures des deux côtés manquants en effectuant des soustractions avec les mesures des côtés connus, mais la stratégie suivante nous éviterait d’avoir à le faire.
Il est à noter que cette stratégie est tout de même envisageable même si nous connaissons la mesure des deux autres côtés de la figure.

Auriez-vous d’autres stratégies à me partager? Il me fera plaisir d’ajouter d’autres exemples de stratégies à cet article! N’hésitez pas à m’écrire si vous avez des questions, des commentaires ou si vous souhaitez partager votre expérience après avoir utilisé ce problème avec vos élèves.
martin.roy005@csssamares.gouv.qc.ca
Lien vers le diaporama qui contient l’ensemble des images présentées dans cet article. (privilégier Microsoft Powerpoint).
Dernière mise à jour de cet article : 3 décembre 2024