Un problème qui nécessite qui nécessite de mobiliser ses connaissances sur le cercle et une bonne dose de réflexion! Un problème accessible pour les élèves de 2e secondaire.
D’autres problèmes similaires pour les élèves de 3e, 4e et 5e secondaire sont également proposés : Le territoire de Fiona et Le bélier.
Pour plus de détails, c’est par ici ⬇️.
On a fabriqué une corde dont la longueur est exactement celle de la circonférence de la Terre à l’équateur. En supposant qu’on la rallonge d’un mètre et qu’on lui fasse faire le tour de l’équateur, toujours à égale distance de la surface de la Terre (on supposera qu’elle est lisse!), quel est le plus grand animal qui pourrait passer sous la corde? Une fourmi? Un lapin? Un tigre? Un éléphant?
Détails sur ce problème ici ⬇️.
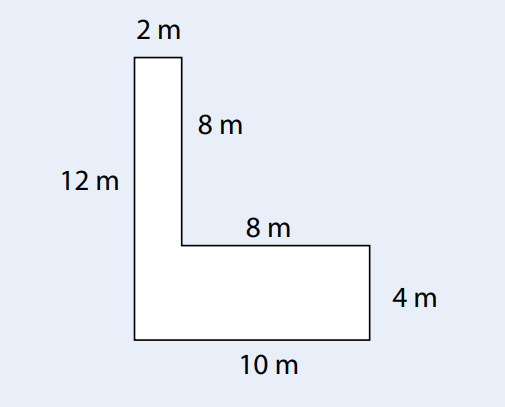
Combien de stratégies différentes êtes-vous en mesure d’identifier pour déterminer l’aire de cette figure? Deux? Trois? Quatre? Davantage? Ce problème est utilisé dans le Référentiel d’intervention en mathématique pour illustrer le concept de flexibilité. Il pourrait être utile pour vulgariser (et valoriser!) ce concept auprès de vos élèves.
Plusieurs exemples de stratégies dans cet article ⬇️.
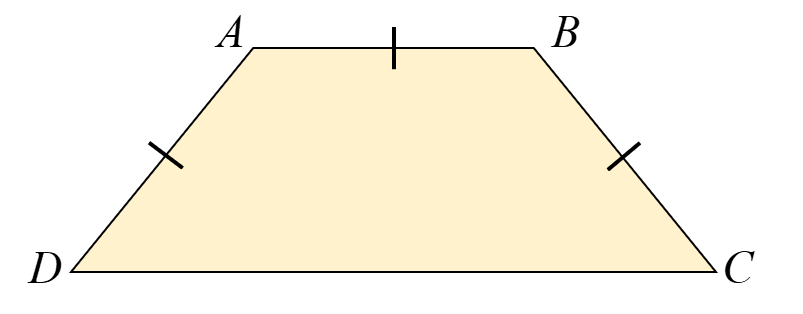
Voici le trapèze ABCD. Sachant que la distance perpendiculaire entre AB et CD est de 8 unités et que la longueur du côté CD est égale à 4 de plus que la moitié de la somme des trois autres côtés, détermine l’aire et le périmètre du trapèze ABCD.
Pour un exemple de solution, c’est par ici ⬇️.
Un problème bien intéressant pour les élèves de 3e secondaire. À l’aide de Pythagore et de manipulations algébriques, ils pourront trouver la solution à celui-ci.
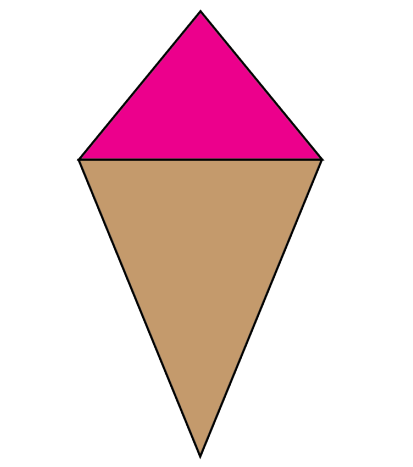
Xavier a fabriqué un bloc de courtepointe en forme de cornet de crème glacée. Le bloc est composé de deux triangles isocèles organisés de façon à former un cerf-volant. (…)
La suite du problème ici ⬇️.
Vous travaillez l’aire des triangles avec vos élèves? Vos élèves ont de la difficulté à identifier la hauteur d’un triangle lorsque celle-ci est à l’extérieur du triangle? Ce n’est pas évident pour vos élèves de comprendre que n’importe quel côté d’un triangle peut être considéré comme sa base? Les puzzles de Sankaku pourraient vous intéresser!
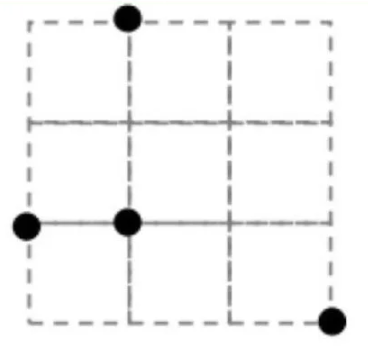
Pour travailler les définitions et caractéristiques des figures planes, les concepts d’angles, de droites parallèles et perpendiculaires et pour travailler avec des figures qui ne sont pas disposées uniquement de manière prototypique. Une activité qui est pertinente sur plusieurs niveaux au secondaire. Serez-vous en mesure de repérer les formes géométriques demandées?
Un environnement pour amener la manipulation d’objets mathématiques à un autre niveau!
De supers problèmes pour développer les compétences de nos élèves en résolution de problèmes!
À la suite d’une demande d’une enseignante pour un corrigé, j’ai créé ce fichier Google Sheet qui permet de vérifier les calculs des élèves selon les nombres qu’ils choisissent. Ça devrait vous épargner des tonnes de calculs! Vous pourrez même faire varier l’intervalle d’un élève à l’autre ou d’un groupe à l’autre.