Les problèmes relatifs aux systèmes d’équations proposés aux élèves sont souvent calqués sur les mêmes squelettes. La disposition ou le type d’informations fournies fait parfois en sorte que le système d’équations nous saute aux yeux. Ça peut être intéressant de proposer aux élèves des problèmes où le système d’équations est un peu plus dissimulé. Voici le problème de la semaine proposé par le CENTRE d’ÉDUCATION en MATHÉMATIQUES et en INFORMATIQUE de l’Université de Waterloo.
Algèbre
Faire de la drill autrement!
Résoudre des équations algébriques, c’est bien! Résoudre les mêmes équations algébriques à travers un labyrinthe, un casse-tête ou un jeu d’évasion, c’est mieux! 😉 Survol de différentes idées pour faire réaliser des exerciseurs à nos élèves de façon plus ludique ou plus engageante. En d’autres termes, changer le contenant sans nécessairement changer le contenu!
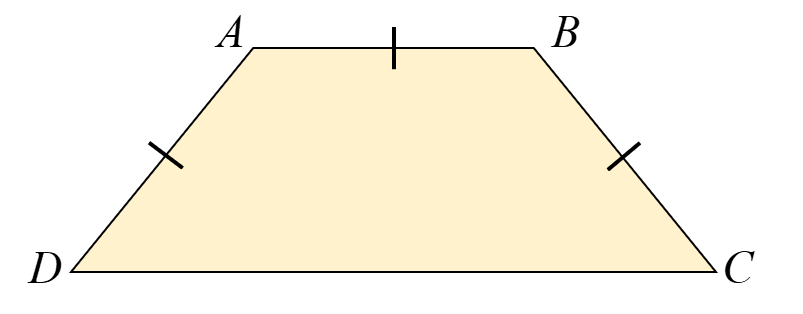
Le trapèze
Voici le trapèze ABCD. Sachant que la distance perpendiculaire entre AB et CD est de 8 unités et que la longueur du côté CD est égale à 4 de plus que la moitié de la somme des trois autres côtés, détermine l’aire et le périmètre du trapèze ABCD.

Pour un exemple de solution, c’est par ici ⬇️.
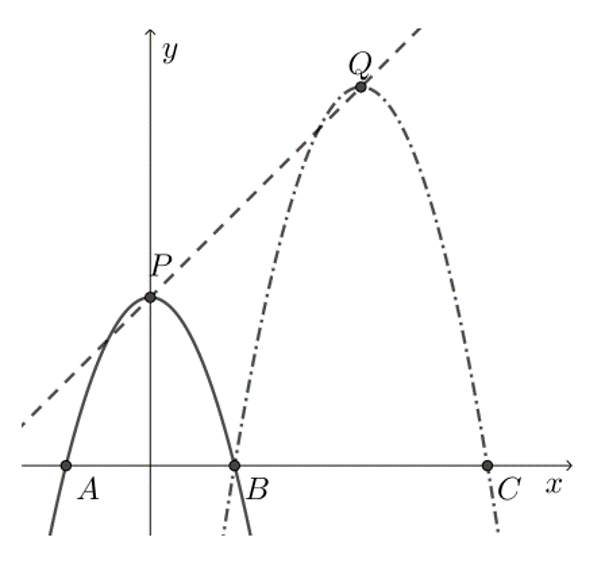
Une parabole qui se déplace
Un problème intéressant pour les élèves en 4SN.
Pour plus de détails, c’est ici ⬇️.
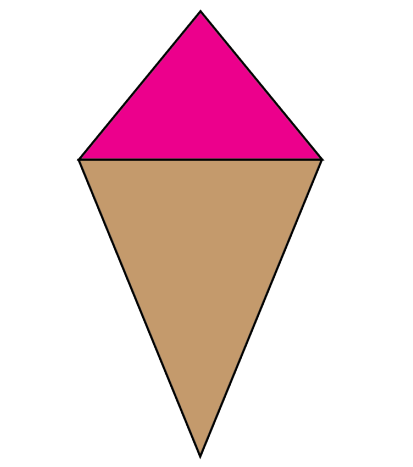
Qui veut de la crème glacée?
Un problème bien intéressant pour les élèves de 3e secondaire. À l’aide de Pythagore et de manipulations algébriques, ils pourront trouver la solution à celui-ci.
Xavier a fabriqué un bloc de courtepointe en forme de cornet de crème glacée. Le bloc est composé de deux triangles isocèles organisés de façon à former un cerf-volant. (…)
La suite du problème ici ⬇️.
Des poignées de main
Un groupe est formé de 12 personnes. Combien de poignées de mains différentes peuvent-ils s’échanger? Et pour un groupe de 20 personnes? Et pour des groupes de n’importe quelle dimension?
Pour plus d’infos sur ce problème ⬇️.
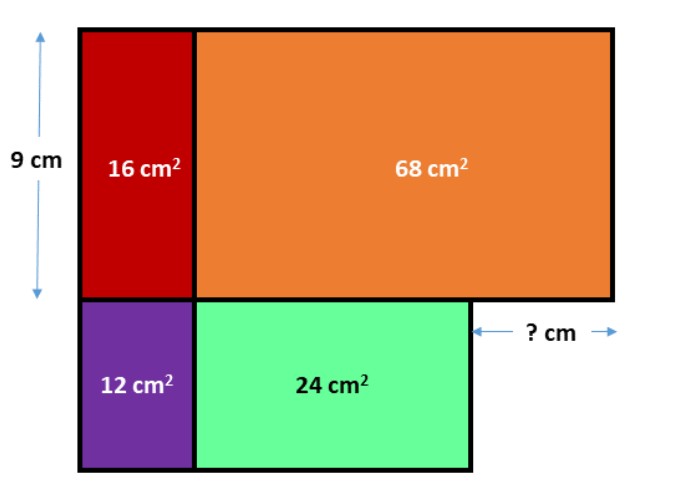
Puzzles de Menseki
Trouvez la valeur du point d’interrogation. Important : vous devez résoudre le puzzle en utilisant SEULEMENT des nombres entiers. Les puzzles de Menseki peuvent paraître banals à première vue, mais vous verrez qu’ils constituent de riches problèmes mathématiques.