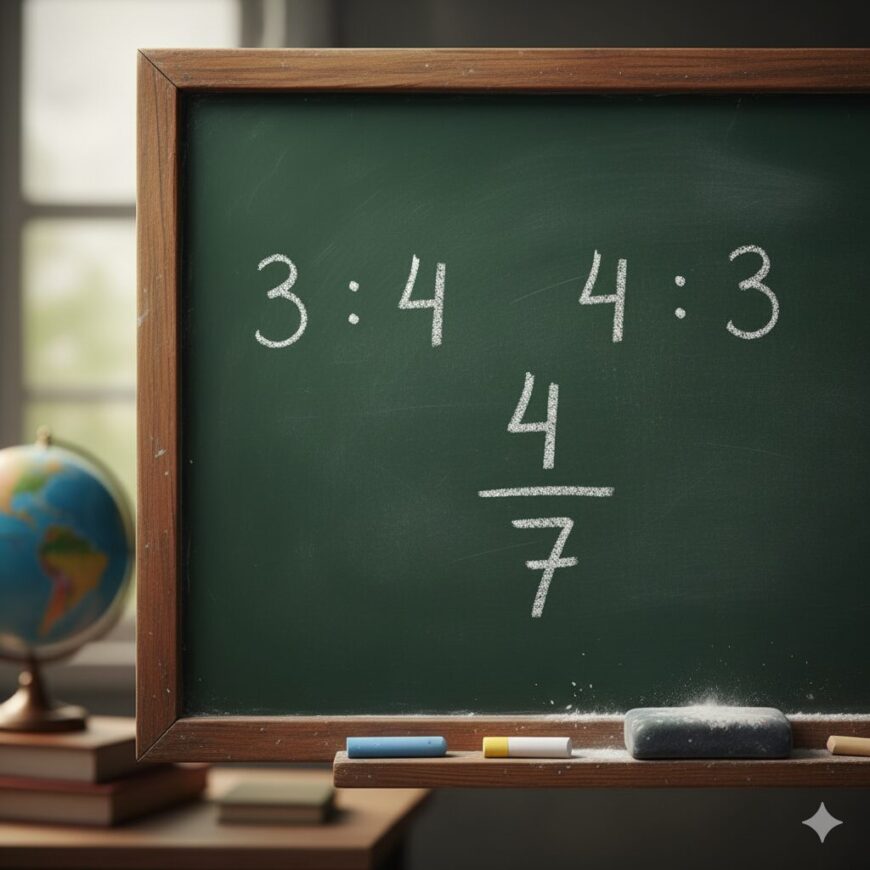Une de vos collègues m’a récemment questionné par rapport à l’écriture des rapports en 2e secondaire (avec les deux points “:” ou avec la barre de fraction) et une certaine incohérence avec ce qui est proposé/enseigné en 4e secondaire quand il est question de point de partage d’un segment.
En résumé, sa question était la suivante : pourquoi un rapport 3 : 4 s’exprime aussi 3/4 en 2e secondaire alors qu’en 4e secondaire avec le point de partage, un rapport partie à partie de 3 : 4 s’exprimera 3/7 en fraction?
J’ai réfléchi à la question et consulté certains ouvrages, en plus de m’entretenir avec certaines personnes à ce sujet. Je vous résume l’essentiel de ce que j’en ai tiré.