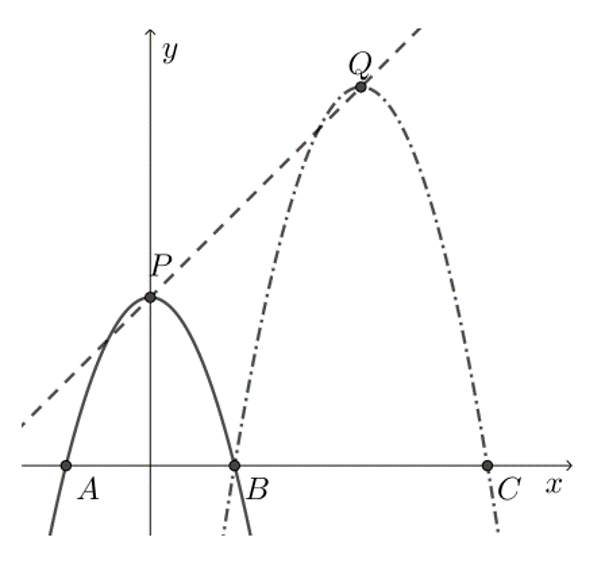
Un problème intéressant pour les élèves en 4SN.
Pour plus de détails, c’est ici ⬇️.

Traduction et adaptation : Martin Roy, avril 2024

Avant de poursuivre la lecture de cet article, je vous invite à tenter de résoudre le problème par vous-même. Vous serez alors assurés que votre raisonnement et vos stratégies ne seront pas influencés par ce qui suit. Si vous ne l’essayer pas par vous-mêmes maintenant, vous pourriez avoir des regrets dans les jours à venir! Voilà, vous êtes avertis! 😁
Exemple de raisonnement approprié
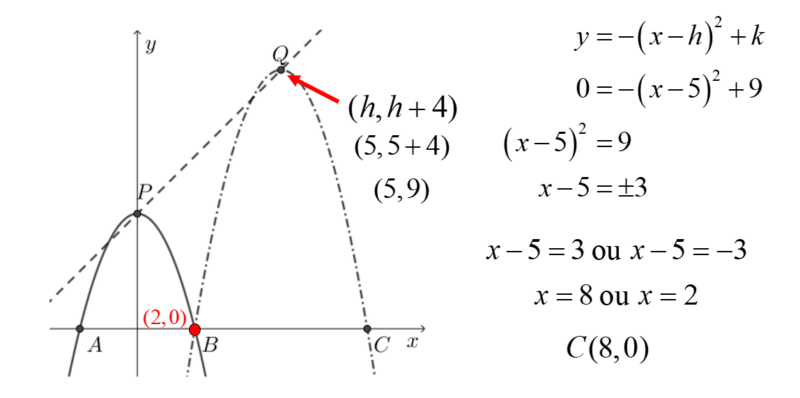
Déterminons d’abord les coordonnées du point B. Nous devons donc trouver les zéros de la parabole dont nous connaissons l’équation.
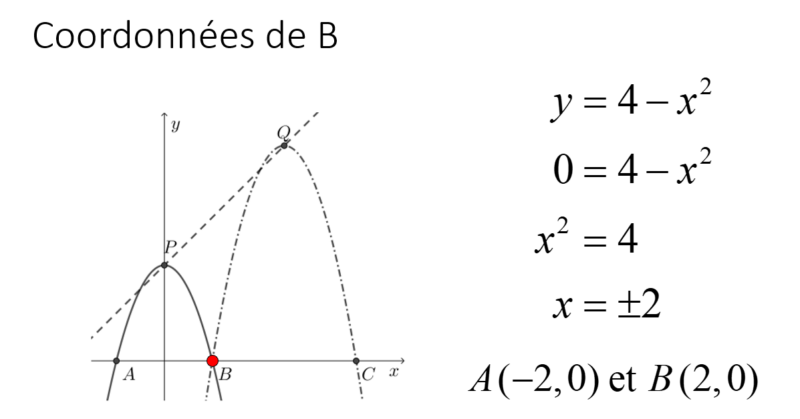
Maintenant que nous connaissons les coordonnées du point B, nous connaissons donc un point de la seconde parabole. Pour le sommet de cette seconde parabole, nous savons qu’il passe par la droite y=x+4. Compte tenu que le sommet (h,k) appartient à la droite y=x+4, nous pouvons déduire que k=h+4. On peut donc substituer ce que l’on connait dans l’équation de seconde parabole.
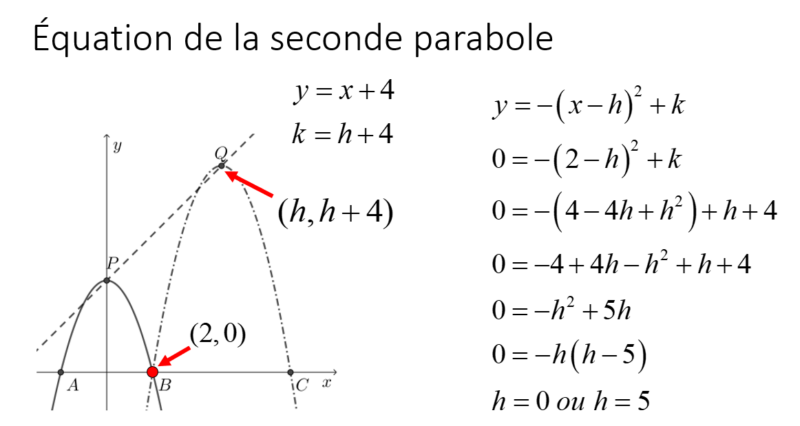
La valeur de h de 0 correspond au point P(0,4) qui est notre parabole initiale. Le valeur que l’on considérera pour notre parabole déplacée est donc h=5. Une fois ce paramètre trouvé, deux stratégies peuvent être utilisées.
1re stratégie : en utilisant l’axe de symétrie de la parabole x=5.
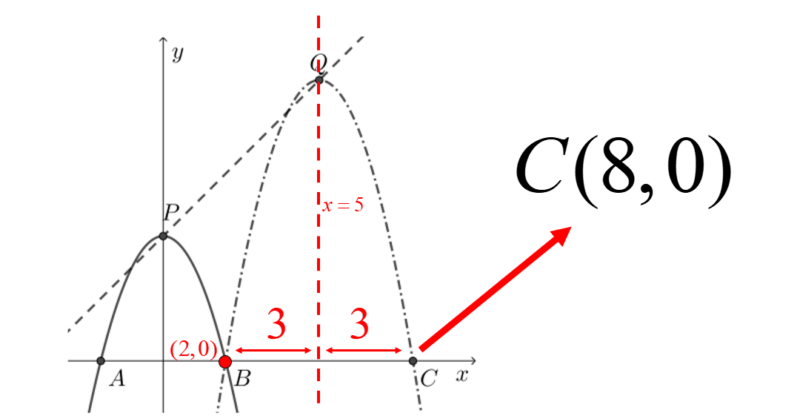
2e stratégie : en utilisant les coordonnées du sommet pour déterminer les zéros. La valeur de l’abscisse du sommet valant 5, son ordonnée vaut donc 9 (h+4).
Lien vers le diaporama contenant l’ensemble de ces images (privilégier Microsoft Powerpoint pour que les animations fonctionnent correctement).
Lien vers la tâche originale et le corrigé du CEMC.
N’hésitez pas à m’écrire si vous avez des questions ou des commentaires! Je suis également très intéressé à recevoir vos exemples de raisonnements ou des traces des raisonnements de vos élèves. Il me fera plaisir d’ajouter d’autres exemples de raisonnements à cet article!
martin.roy005@csssamares.gouv.qc.ca
Dernière mise à jour de cet article : 28 novembre 2024
Une ressource très riche en problèmes!
Chaque semaine, le CENTRE d’ÉDUCATION en MATHÉMATIQUES et en INFORMATIQUE de l’Université de Waterloo partage de riches problèmes (pour la 3e à la 12e année). Les solutions de chacun de ces problèmes sont partagées une semaine plus tard.
Lien pour avoir accès aux problèmes en français
Lien pour avoir accès aux problèmes en anglais (vous aurez ainsi accès aux problèmes 11e/12e année)
Archives des problèmes des années 2022-2023 et 2023-2024 (français)
Archives des problèmes des années 2022-2023 et 2023-2024 (anglais avec les problèmes 11e/12e année)
Les archives contiennent également l’ensemble des solutions des problèmes!